Vierkante bellen

Jaren geleden, ik was toen vierdejaars student aan de Technische Hogeschool Eindhoven, kreeg ik bij wijze van stage-opdracht het volgende probleem te verwerken. En om eerlijk te zijn, ik was toentertijd niet in staat om het op een goede manier aan te pakken, laat staan op te lossen. Met name van een toepasselijke theorie kwam hoegenaamd niets terecht. O ja, wel allerlei ingewikkelde formules over tensoren op gekromde oppervlakken, een stuk "fundamentele bellentheorie" dat uiteindelijk nergens op bleek te slaan.

Gegeven is een blokje perspex met daarin uitgeboord twee capillaire buisjes, één buisje horizontaal door het blokje heen, één buisje vertikaal daarop, loodrecht uitkomend op het eerste. De capillairen komen samen op één punt, en vormen daar een omgekeerde hoofdletter T, vandaar ook de naam "T-stuk". De diameter van de capillairen bedraagt 1.0 millimeter. Water stroomt van rechts naar links door het horizontale buisje, lucht stroomt van boven naar onder door het vertikale buisje. Waar de twee media elkaar ontmoeten vormen zich luchtbellen. Het mengsel van lucht en water stroomt via het horizontale buisje naar buiten. Hieronder volgt een schets van het T-stuk, met daarin het beeld van een aangroeiende luchtbel, gezien van opzij:

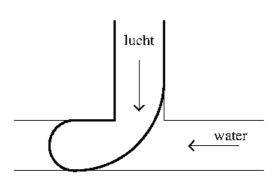
Onafhankelijke variabelen zijn de volumenstromen van lucht en water, ook wel genoemd luchtdebiet $F_L$ en waterdebiet $F_W$. Afhankelijk variabelen zijn de frequentie $f$ van de belvorming en het luchtbelvolume $V_L$. (Overigens zou men met evenveel recht uit kunnen gaan van het volume van de "water"bellen $V_W$). Zoals men licht kan inzien, bestaat er een eenvoudig verband tussen de frequentie en de belvolumes: $V_L=F_L/f$ en $V_W=F_W/f$. De bedoeling was om ook proefondervindelijk vast te stellen of er een verband bestaat tussen de onafhankelijke en de afhankelijke variabelen. Gemeten waarden zijn weergegeven in onderstaande tabel. De waarde gemerkt met (*) was oorspronkelijk 1.9, hetgeen waarschijnlijk berust op een schrijffout tijdens de metingen.

Lucht (mm3/s)	Water (mm3/s)	Frekwentie (1/s)
44	56	31
62	50	35
66	45	35
78	45	37
140	41	43
149	42	44.5
29	70	25
18	79	20
9	98	14.5
6	133	11
21	177	42
18	180	35
14	199	30
7	205	19 *
9	232	22
1	235	2.4
33	145	47
49	135	57
55	135	62
62	124	60
66	117	65
91	117	80
95	152	80
96	109	75
99	108	73
120	112	90
122	92	76
145	115	92
146	98	88
157	98	97
169	100	95

Vervolgens werd van mij verwacht dat ik de metingen zou verklaren met behulp van een mathematisch model. Kosten nog moeite werden gespaard. Er werd een film van het verschijnsel gemaakt, teneinde het beter te kunnen bestuderen. Na het zien van de film, loste niet ik, maar een vriend en medestudent van me, het probleem in 5 minuten op. Hij schreef de oplossing op de achterkant van een bierviltje (: we zaten in het lokale studentencafé).

Jacques deed een paar aannamen die het hele probleem drastisch vereenvoudigden. Achteraf moeten we vaststellen dat hij intuïtief heel goed begrepen moet hebben waar het bij het ontwerpen van een mathematisch model op aan komt. Laten we om te beginnen maar eens aannemen dat de vorming van de luchtbellen in het geheel niet afhangt van de oppervlaktespanning, en daarmee ook niet van een eventuele kromming van de oppervlakken. Dan is het in feite niet zo belangrijk welke vorm het beloppervlak precies bezit (dit in schrille tegenstelling tot wat ik altijd had gedacht). Wanneer de bellen niet rond behoeven te zijn, dan kunnen we ons voor het gemak indenken dat ze in plaats daarvan, schrik niet: vierkant zijn. Dit nu blijkt de cruciale stap te wezen. Het is duidelijk dat men onmogelijk zover kan komen zonder een dosis verbeeldingskracht, zonder zich los te maken van de direkte ogenschijnlijke ervaring. Wat hier gebeurt overstijgt het vermogen van een simpel waarnemingsinstrument. Hier komt een mens aan te pas. Er is niet langer sprake van abstraktie, maar van idealisatie.

Voortbordurend op de vierkante bellen kan men vervolgens een geïdealiseerd scenario opstellen voor de belvorming in het T-stuk. Aangenomen wordt dat een en ander, modelmatig, in zijn werk gaat als weergegeven in de volgende figuur:

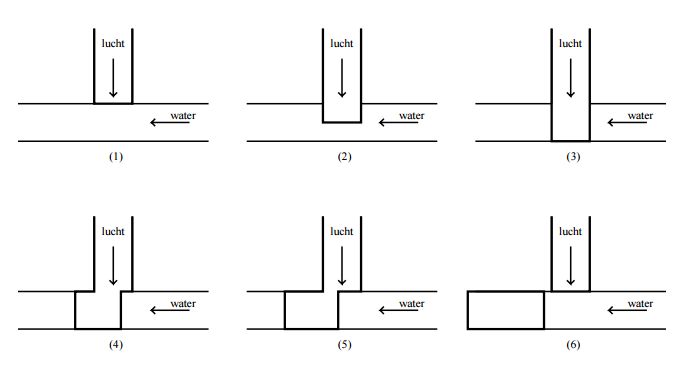
Het idee is dus dat eerst de bel door de luchtstroom tot tegen de overzijde van het waterkanaal wordt gedrukt (fase 1-3), en daarna door de waterstroom over de breedte van het luchtkanaal wordt afgeknepen (fase 4-6). Aan de hand van dit geïdealiseerde beeld is het zowaar mogelijk een zinvolle berekening op te zetten:
De tijd nodig voor fase 1-3 = diameter water-kanaal / lucht-snelheid
De tijd nodig voor fase 4-6 = diameter lucht-kanaal / water-snelheid
Ofwel: $t13=d/(F_L/A)$ ; $t46=d/(F_W/A)$.
Zodat: $t13=V_O/F_L$ ; $t46=V_O/F_W$.
Hierin is $A=$ stromingsdoorsnede, $d=$ kanaaldiameter.
Zodat $V_O=$ een soort "nul"volume, waarbij $V_O=A d$ .
De totale tijd nodig voor belvorming is: $t16=t13+t46=$ $$ 1 / f = V_O ( 1/F_L + 1/F_W ) $$ Het volume van de luchtbel is dus: $$ V_L = F_L / f = V_O ( 1 + F_L/F_W ) $$ De enige nog onbekende grootheid in deze formule is $V_O$ .

Dit "nulvolume" kan op twee manieren worden bepaald. De eerste manier gaat uit van een ruwe schatting: het volume moet inliggen tussen dat van een bol en een cylinder. Uitgaande van het gegeven dat de diameter van de capillairen $1 mm$ is, vinden we voor de cylinder: $\pi d^3/4=0.785$ en de bol: $\pi d^3/6=0.52 $.

Op de tweede plaats kunnen we proberen het model in overeenstemming te brengen met de metingen. Stel $x=F_L/F_W$ en $y=V_L$. Een kleinste kwadraten aanpassing geeft: $$ \sum_{i=1}^{N} \{V_O [1 + x_i] - y_i \}^2 = \mbox{minimaal} $$ waarin $N$ het aantal meetpunten is. Dit is een kwadratische funktie in $V_O$: $$ A V_O^2 - 2 B V_O + C = minimaal $$ Met: $ A = \sum_{i=1}^{N} (1+x_i)^2 $ \ ; \ $ B = \sum_{i=1}^{N} (1+x_i) y_i $, $ C = \sum_{i=1}^{N} y_i^2 $ . Zoals bekend wordt het minimum van deze parabool, met $V_O$ als onafhankelijke variabele, gevonden voor: $ V_O = B/A $. Ofwel: $$ V_O = \frac{\sum_{i=1}^{N} (1+x_i) y_i}{\sum_{i=1}^{N} (1+x_i)^2} $$ Dit geeft uit de metingen een waarde van $V_O = 0.6934510 = 0.7 mm^3$. Zodat de experimentele waarde inderdaad tussen de ruwe theoretische waarden in ligt.

Zetten we tenslotte metingen en berekeningen samen uit in een grafiek. Dan is onder andere te zien dat voor de kleinste belvolumes de metingen systematisch afwijken van de berekening. Dit kan worden verklaard doordat bij een krachtiger waterstroom de bellen eerder worden "afgeknepen", dat is voordat hun nulvolume $V_O$ wordt bereikt.

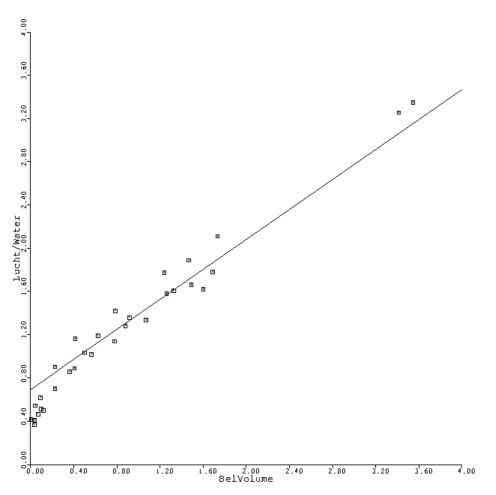
We hebben afgeleid de fundamentele natuurwet voor de vorming van bellen in een T-stuk: $V_L=V_O(1 + F_L/F_W)$. Een wet die overtuigt door eenvoud en elegantie. Er gaat een zekere bekoring uit van zulke formules, zegt men, en men vraagt zich af wat in diepste wezen toch de grond is van deze schoonheid. In het geval van de belvorming is het antwoord duidelijk: de schoonheid van de gevonden formule is uitsluitend te danken aan de dramatische vereenvoudiging die we hebben toegepast. De schoonheid ontstaat niet doordat we de werkelijkheid in al haar bijzonderheden hebben gevat, maar juist doordat we hebben afgezien van de meeste aspekten van de werkelijkheid, niet doordat we de hele waarheid hebben nagestreefd, maar juist doordat we die waarheid niet hebben nagestreefd. Het paradoxale is dat we daardoor toch dichter bij "de waarheid" zijn gekomen. Immers, het resultaat is kwantitatief, stemt goed overeen met de experimenten, kortom is precies wat men van een (klein) stukje wetenschap mag verwachten.

Waarom zo veel aandacht geschonken aan een relatief onbenullige "toepassing" zoals deze? Ik had het hierboven dan wel over de fundamentele natuurwet van de belvorming in een T-stuk, maar dat zal ongetwijfeld bedoeld zijn als een beeldspraak. Schrijver dezes gaat toch niet vertellen dat een formule voor onnozele belletjes, hoe aardig hij er ook uitziet, eenzelfde status heeft als bijvoorbeeld de wetten van de Newton of de Lorenz transformaties? Mis. Dat gaat deze schrijver dus wel vertellen. Een van de kernpunten is namelijk dat, naarmate men er dieper over nadenkt, er geen wezenlijk onderscheid meer gemaakt kan worden tussen "fundamenteel" en "toegepast" onderzoek. Als we wat verder zijn, zal gaandeweg blijken dat dit onderscheid steeds moeilijker is vol te houden, en tenslotte als vanzelf verdwijnt. Welliswaar kan men verdedigen dat $ F=m.a $ een breder toepassingsgebied heeft dan $V_L=V_O(1 + F_L/F_W)$, en in die zin fundamenteler is. Maar ik hou staande dat het daarbij gaat om een gradueel, niet om een essentieel verschil.

Men kan niet ergens tussen de natuurwetten een grens trekken en zeggen: aan deze kant is alles exakt, en aan die kant is alles een benadering.

Ook de schoonheid van "echte" natuurwetten berust zodoende op zinsbegoocheling. Ze is louter het resultaat van vereenvoudiging, een simplifikatie die door ons mensen zelf, al dan niet doelbewust, wordt aangebracht, en die in wezen de werkelijkheid geweld aandoet, in plaats van deze te omvatten. Het zal me straks een waar genoegen zijn om een en ander nog eens flink aan te zetten, door bij voorkeur grofstoffelijke werktuigbouwkundige toepassingen te berde te brengen, als illustratie van wat het betekent een "fundamentele natuurwet" in handen te hebben.