overzicht overview
Het schandaal van de propositielogica
Geachte heer Rutten /
Beste Emanuel,
Mag ik mij even voorstellen. Mijn naam is Han de Bruijn,
72 jaar, ingenieur technische natuurkunde, afgestudeerd theoretische fysica.
Mijn twee voornaamste bezigheden (naast zaken van huishoudelijke en sociale aard)
zijn wiskunde en muziek.
Daarnaast voer ik soms discussies op het Sterrenstof forum. Daar kwam een zekere Emanual Rutten ter sprake:
1 JULI, 2019 OM 3:40 PM.
Toen ging ik graven.
Het probleem van de materiële implicatie speelt bij mij als sinds mijn afstuderen, en dan spreek ik over 1973, uw geboortejaar!
Klik op:

Volgens mij is er dus wel degelijk een oplossingsrichting, zoals ook aangeduid op Sterrenstof: de IF .. THEN .. ELSE .. in computertalen.
Nemen we de Nederlandse presentatie "Het schandaal van de propositie logica"
slide nummer 58: $(P \Rightarrow R) \vee (Q \Rightarrow R)$.
In gewone omgangstaal is dit, pertinent onjuist:
Uit het feit dat Jan ouder is dan 20 volgt dat zijn leeftijd tussen 20 en 30 ligt
OF uit het feit dat hij jonger is dan 30 volgt dat zijn leeftijd tussen 20 en 30 ligt.
In de Engelstalige versie staat er:
Brigitte can mix green with yellow paint
or Brigitte can mix green with blue paint.
In een boek over compiler bouw [ David Gries, "Compiler Construction for Digital Computers", John Wiley & Sons, 1971 ] lezen wij:
c OR d wordt gedefinieerd door IF c THEN TRUE ELSE d
c AND d wordt gedefinieerd door IF c THEN d ELSE FALSE
NOT c wordt gedefinieerd door IF c THEN FALSE ELSE TRUE
c ==> d wordt gedefinieerd door IF c THEN d ELSE TRUE
c wordt gedefinieerd door IF c THEN TRUE ELSE FALSE
De gewraakte uitdrukking $(P \Rightarrow R) \vee (Q \Rightarrow R)$ wordt hiermee:
if (if P then R else TRUE) then TRUE else (if Q then R else TRUE)
In de bijlage vindt u een stroomdiagram
dat overeenkomt met deze opeenvolging van instructies.
In dit stroomdiagram is de tweede variabele R met rood onderstreept. Want let op! Hier komt de clou!
Welke waarden u ook kiest voor P, Q en R in de betekenis van hierboven, de onderstreepte R wordt nooit uitgevoerd!
Maar we hebben nog meer geluk.
In de meeste moderne programmeertalen zijn "boolean expressions" namelijk automatisch onderhevig aan "lazy evaluation".
Daarom kunnen we de sequentiële uitdrukking van hierboven eenvoudig vervangen door het combinatorische equivalent:
$((\neg P) \vee R) \vee ((\neg Q) \vee \underset{\color{red}{\bf -}}{R}(R))$.
Met een kleine aanpassing voor de tweede variabele $R$: de functie $\underset{\color{red}{\bf -}}{R}(R)$ is identiek aan $R$
maar bevat een alarm melding: ' waargenomen! '.
Een klein programmaatje in Pascal moet nog meer duidelijk maken waar de clou zit: inderdaad wordt de melding nooit gegeven!
program de_clou;
function r_(r : boolean) : boolean;
begin
Write(' waargenomen! ');
r_ := r;
end;
procedure test;
var
p,q,r : boolean;
k : integer;
L : double;
begin
Writeln('P':6,'Q':6,'R':6,'(P=>R)v(Q=>R)':16);
Writeln('-----------------------------------');
for k := 1 to 3 do
begin
L := 10*k+5;
p := (L >= 20); q := (L <= 30); r := (p and q);
Writeln(p:6,q:6,r:6,((not p) or r) or ((not q) or r_(r)):12);
{ if (if p then r else true) then true else (if q then r else true) }
end;
end;
begin
test;
end.
Uitvoer (let op afwezigheid alarm):
P Q R (P=>R)v(Q=>R)
-----------------------------------
FALSE TRUE FALSE TRUE
TRUE TRUE TRUE TRUE
TRUE FALSE FALSE TRUE
Het feit dat de opdracht $\underset{\color{red}{\bf -}}{R}(R)$ nooit kan worden uitgevoerd komt geheel en al overeen
met het besef van onzinnigheid in de omgangstaal.
$\underset{\color{red}{\bf -}}{R}(R)$ is op geen enkele wijze waarneembaar; het is alsof deze instructie er simpelweg niet is.
Dus wat er in feite staat is dit: $((\neg P) \vee R) \vee (\neg Q)$.
Uit het feit dat Jan ouder is dan 20 volgt dat zijn leeftijd tussen 20 en 30 ligt
OF hij is niet jonger dan 30
Dit lijkt mij geen schandalige conclusie meer!
Met vriendelijke groet,
Han de Bruijn
Beste Emanuel,
Aanleiding to mijn email was een bericht
op het Sterrenstof forum over deze publicatie:
Het kosmologisch argument - E. Rutten.
De publicatie genoemd in je email lijkt op het eerste gezicht van soortgelijke strekking:
Atomism, Causalism and the Existence of a First Cause - E. Rutten.
Zelf ben ik absoluut geen atheïst en heb geen a priori oordeel over argumenten die het bestaan van God aannemelijk proberen te maken.
Maar ik heb beide artikelen slechts vluchtig doorgelezen, getuige bijvoorbeeld
deze reactie.
Met degene die jouw publicatie ter sprake bracht (Ubbo) heb ik vervolgens een tamelijk vruchteloze discussie gevoerd over
causaliteit.
Waarbij moet worden aangetekend dat mijn begrip, van wat causaliteit eigenlijk is, aanzienlijk afwijkt van wat anderen ervan denken:
Maar om nog even terug te komen op "Het schandaal van de propositielogica".
We hebben gezien dat de gewraakte uitdrukking $(P \Rightarrow R) \vee (Q \Rightarrow R)$ equivalent is met $((\neg P) \vee R) \vee ((\neg Q) \vee R)$.
Dus er staat in feite: $((\neg P) \vee (\neg Q) \vee (R \vee R))$. De laatste R is overbodig: $(R \vee R = R)$. Dus er staat: $(P \Rightarrow R) \vee (\neg Q)$.
Het heeft er de schijn van dat de logica van de omgangstaal superieur is aan de mathematische logica om de volgende reden: EFFICIENCY.
De uitdrukking $(P \Rightarrow R) \vee (Q \Rightarrow R)$ is ondoelmatig / inefficiënt, omdat ze twee keer hetzelfde poneert: $R \vee R$.
Onze logische intuitie "weet" dat en verwerpt dit soort uitdrukkingen. Zou je jezelf in deze conclusie kunnen vinden?
Hartelijke groet,
Han
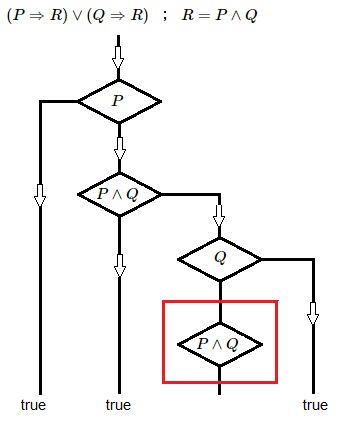
Nog even een andere blik op ons oude probleem, met 0 = FALSE en 1 = TRUE:
$ (P \Rightarrow R) \vee (Q \Rightarrow R) \quad \mbox{met} \quad R = (P \wedge Q) $
Maar dan sequentiëel opgevat, alle mogelijkheden op een rijtje:
if (if P then R else 1) then 1 else (if Q then R else 1) : algemeen
if (if 0 else 1) then 1 [ ] : P = 0
if (if 1 then 0 ) else (if 0 [ ] else 1) : P = 1, Q = 0
if (if 1 then 1 ) then 1 [ ] : P = 1, Q = 1
De tweede instantie van R is bij alle (0,1) specificaties een lege plek.
Dit betekent dat de tweede instantie van R
- in de meest letterlijke zin - niet waarneembaar is.
Het bijbehorende stroomdiagram is hiermee in overeenstemming:
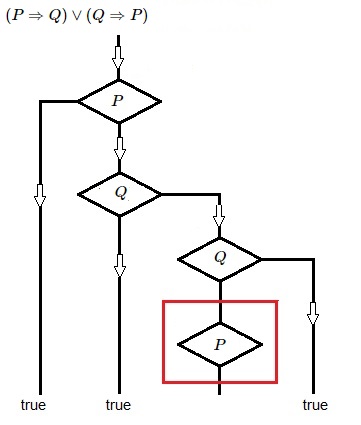
Beschouw de tautologie $(P \Rightarrow Q) \vee (Q \Rightarrow P)$.
Deze is identiek aan $(\neg P) \vee Q \vee (\neg Q) \vee P$
en is dus combinatorisch heel erg waar.
De sequentiële versie is,
met 0 = FALSE en 1 = TRUE en alle mogelijkheden op een rijtje:
if (if P then Q else 1) then 1 else (if Q then P else 1) : algemeen
if (if 0 else 1) then 1 [ ] : P = 0
if (if 1 then 0 ) else (if 0 [ ] else 1) : P = 1, Q = 0
if (if 1 then 1 ) then 1 [ ] : P = 1, Q = 1
De tweede instantie van P is dus niet waarneembaar.
Zoals ook duidelijk te zien is in het stroomdiagram:
Nog een ander "schandalig" voorbeeld tot slot.
Wat te denken van de logische tautologie dat uit een paradox alles te bewijzen valt:
$(P \wedge (\neg P)) \Rightarrow Q$.
In de sequentiële opvatting komt dit neer op:
if FALSE then Q else TRUE
Het is duidelijk dat een computerprogramma nooit de instructie Q zal bereiken.
Dit is waarschijnlijk ook zo in onze hersenen.
De tautologie $(P \wedge (\neg P)) \Rightarrow Q$ is daarom onzin:
uit een paradox valt niet alles te bewijzen. Q is namelijk - alweer - niet waarneembaar.
Niet alle propositielogica is schandalig.
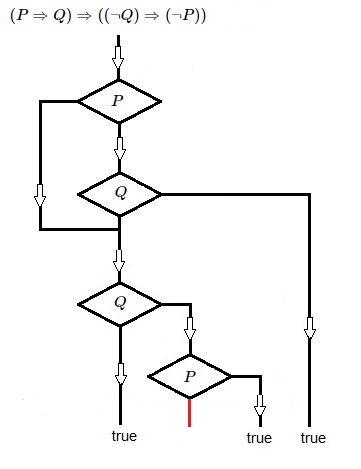
De hoogste tijd voor een tegenvoorbeeld: $(P \Rightarrow Q) \Rightarrow (\neg Q \Rightarrow \neg P)$.
if (if P then Q else 1) then (if -Q then -P else 1) else 1 : algemeen
if (if 0 else 1) then (if 1 then 1 ) : P = 0, Q = 0
if (if 0 else 1) then (if 0 else 1) : P = 0, Q = 1
if (if 1 then 0 ) else 1 : P = 1, Q = 0
if (if 1 then 1 ) then (if 0 else 1) : P = 1, Q = 1
Alle instanties van P en Q zijn dus waarneembaar. Alle nuttige paden leiden naar de waarheid.
Deze tautologie is daarom ook in de omgangstaal aanvaardbaar en zinvol. Het stroomdiagram is: