Quotient Function

$ \def \half {\frac{1}{2}} \def \EN {\quad \mbox{and} \quad} \def \hieruit {\quad \Longrightarrow \quad} \def \slechts {\quad \Longleftrightarrow \quad} $ Suppose the off-diagonal coefficients at the fine grid are $a$ and $b$, and the off-diagonal coefficients at the coarser grid are $a'$ and $b'$, then we know from the chapter about "Persistent Schemes" that the following relationships hold: $$ \frac{a'}{b'} = \left( \frac{a}{b} \right)^2 \EN \frac{a}{b} = \sqrt{ \frac{a'}{b'} } $$ It is inferred that the relative magnitude of the coefficients $a$ and $b$ is persistent through grid coarsening and grid refinement: \begin{eqnarray*} a < b & \slechts & a' < b' \\ a = b & \slechts & a' = b' \\ a > b & \slechts & a' > b' \end{eqnarray*} With grid coarsening, the fraction $a/b$ is subject to the function $x'=x^2$. The outcome of which can be subject to another grid coarsening $x''=x'^2$, to another grid coarsening $x'''= x''^2$ and so on and so forth. Resulting in an expression: $$ \left( \left( \left( \left( ... x^2 \right)^2 \right)^2 ... \right)^2 \right)^2 = \lim_{N \rightarrow \infty} \! \! x^{2^N} = 0 \: , 1 \: , \: \infty \quad \mbox{for } \; x < 1 , x = 1 , x > 1 $$ With grid refinement, the fraction $a/b$ is subject to the function $x'=\sqrt{x}$. The outcome of which can be subject to another grid refinement $x''=\sqrt{x'}$, to another grid refinement $x'''=\sqrt{x''}$ and so on and so forth. Resulting in an expression: $$ \sqrt{ \sqrt{ \sqrt{ \sqrt{ \sqrt{ ... \sqrt{x}}}}}} = \lim_{N \rightarrow \infty} \! \! \sqrt[2^N]{x} = 1 \quad \mbox{for } \; x > 0 $$ Click On Pic for viewing the accompanying PostScript code of this picture:

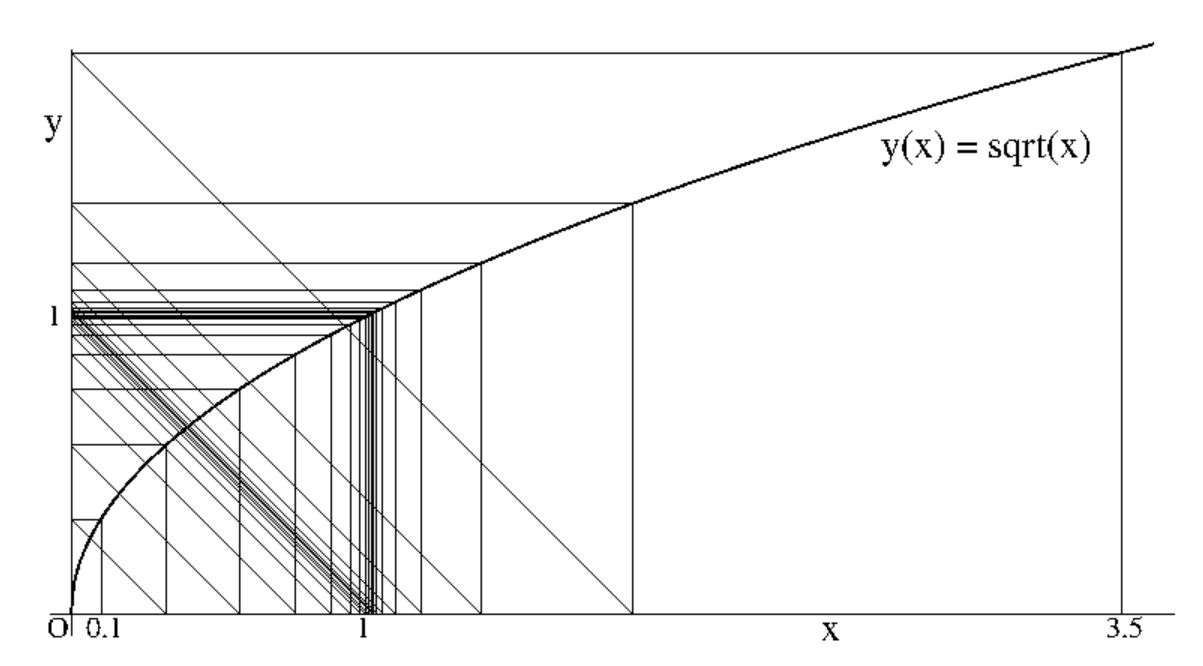
It is kind of a custom to say, nowadays, that the function $y=\sqrt{x}$ has an attractor for $x=y=1$. The practical meaning is that, at infinitely refined grids, $a$ and $b$ will become equal: $a = b$ for grid $\rightarrow \infty$-dense. (Provided that $a \ne 0$ and $b \ne 0$; for if else they will remain zero forever.) The point $(1,1)$ itself is a stable stationary point: any point in the neighbourhood will become more and more "equal" to it and the point $(1,1)$ itself does not change with further iterations.
It is seen, on the contrary, that the point $x=y=1$ of the inverse function $y=x^2$ is not an attractor, but more like a repeller instead. Values smaller than $1$ are pushed towards zero, while values greater that $1$ are pushed towards infinity. The point $x=y=1$ itself is a stationary point, but it is highly unstable.
If a grid becomes 2 times coarser, then the new quotient of $a$ and $b$ will be related to the old one by: $(a/b) := (a/b)^2$. If a grid becomes $1/2$ times coarser, then the new quotient of the off-diagonal elements will be related to the old one by: $(a/b) := (a/b)^{1/2}$. We could also have written: $$ \frac{a}{b}(2.dx) = \left[ \frac{a}{b}(dx) \right]^2 \EN \frac{a}{b}(\half dx) = \left[ \frac{a}{b}(dx) \right]^{1/2} $$ We seek to generalize these results, where a relationship as the following comes into mind: $$ \frac{b}{a} \: (p.dx) = \left[ \frac{b}{a} \: (dx) \right]^p \quad \mbox{for any real number} \; p $$ An interpretation for negative numbers $p$ can be obtained as follows. Consider a one-dimensional grid and suppose that it is traversed in the reverse direction. Thus, instead of numbering grid points from the left to the right, they are numbered from the right to the left. By this "inverse" transformation, any matrix coefficient $a_{ij}$ with $i > j$ will be mapped upon a coefficient $a_{ji}$ and any coefficient $a_{ji}$ will be mapped upon a matrix coefficient $a_{ij}$. Using uniform meshes, we see that coefficients $a$ are transformed into coefficients $b$ and coefficients $b$ are transformed into coefficients $a$. This means that fractions $a/b$ will be transformed into fractions $b/a$ and vice versa. But travelling the grid in reverse order also means that we are using increments $(-dx)$ instead of increments $(+dx)$. Therefore we can write: $$ \frac{a}{b}(-dx) = \frac{b}{a}(dx) = \left[ \frac{a}{b}(dx) \right]^{-1} \EN \frac{b}{a}(-dx) = \frac{a}{b}(dx) = \left[ \frac{b}{a}(dx) \right]^{-1} $$ For $dx = 0$ it follows that $-dx = +dx$, hence: $$ \frac{a}{b}(0) = \frac{b}{a}(0) \hieruit \frac{a}{b}(0) = \frac{b}{a}(0) = 1 $$ This is in close agreement with the observation that the quotient of the off- diagonal terms has an attractor $(0,1)$ in the function for mesh refinement.
It could be interesting to study the quotient of the off-diagonal coefficients, for the limiting case of an immensely refined grid. It is seen in the above figure that the refinement function becomes more and more dense in the neighbourhood of its attractor. It is suspected that the function may be continuous, or even differentiable, in this region. Assume that for a certain mesh-spacing $K$ there exists a certain number $L$ such that: $$ \frac{b}{a}(K) = L $$ On ground of the theory as it has been developed so far, one can safely write: $$ \frac{b}{a}(K) = \frac{b}{a} \left( 2^N. \frac{K}{2^N} \right) = \left[ \frac{b}{a} \left( \frac{K}{2^N} \right) \right]^{2^N} = L \slechts \frac{b}{a} \left( \frac{K}{2^N} \right) = L^{1/2^N} $$ By definition, the fraction $b/a$ is continuous for its argument $=0$ if there does exist a number $\delta(\epsilon)$ in such a way that, for any positive $\epsilon$: $$ \left| \frac{b}{a}(\delta) - \frac{b}{a}(0) \right| < \epsilon $$ But we know that: $b/a(0)=1$. Identify $\delta = K/2^N$, then the condition for continuity will be fulfilled if: $$ \left| \frac{b}{a} (\delta) - 1 \right| = \left| L^{1/2^N} - 1 \right| < \epsilon \quad \slechts $$ $$ \left\{ \begin{array}{c} L^{1/2^N} - 1 < \epsilon \slechts L < (1 + \epsilon)^{2^N} \quad \mbox{if} \quad L \ge 1 \\ 1 - L^{1/2^N} < \epsilon \slechts L > (1 - \epsilon)^{2^N} \quad \mbox{if} \quad L \le 1 \end{array} \right. $$ $$ \left. \begin{array}{c} \slechts ln(L) < 2^N.ln(1+\epsilon) \quad \mbox{(positive)} \\ \slechts ln(L) > 2^N.ln(1-\epsilon) \quad \mbox{(negative)} \end{array} \right\} \slechts 2^N > \frac{ln(L)}{ln(1 \pm \epsilon)} $$ Where the $\pm$ sign is such that the quotient of the two logarithms is always positive (: $1+\epsilon$ for $L>1$, $1-\epsilon$ for $L<1$). We see that, with a suitable choice of $N=N(\epsilon)$: $$ \delta(\epsilon) = \frac{K}{2^N} < K \frac{ln(1 \pm \epsilon)}{ln(L)} \hieruit \left| \frac{b}{a}(\delta) - \frac{b}{a}(0) \right| < \epsilon $$ Which proves that the refinement function for the quotient of the off-diagonal elements is continuous in its attractor.
Now assume that the number $\epsilon$ has been selected in such a way that: $$ 2^N = \frac{ln(L)}{ln(1 \pm \epsilon)} \slechts 1 \pm \epsilon = L^{1/2^N} \slechts \left\{ \begin{array}{c} \epsilon = L^{1/2^N} - 1 \quad \mbox{if} \quad L \ge 1 \\ \epsilon = 1 - L^{1/2^N} \quad \mbox{if} \quad L \le 1 \end{array} \right. $$ Then we find two expressions for the derivative of the Quotient Function in its attractor $(0,1)$: $$ \delta = K \frac{ln(1 + \epsilon)}{ln(L)} \EN \frac{b}{a}(\delta) - 1 = \epsilon \hieruit \left[ \frac{b}{a}(\delta) - \frac{b}{a}(0) \right] / \delta = \frac{\epsilon.ln(L)}{ln(1 + \epsilon).K} \\ $$ $$ \delta = K \frac{ln(1 - \epsilon)}{ln(L)} \EN 1 - \frac{b}{a}(\delta) = \epsilon \hieruit \left[ \frac{b}{a}(\delta) - \frac{b}{a}(0) \right] / \delta = - \frac{\epsilon.ln(L)}{ln(1 - \epsilon).K} $$ By continuously enlarging $N$, we find that $\epsilon \rightarrow 0$ and: $$ \lim_{\epsilon \rightarrow 0} \frac{\pm \epsilon.ln(L)}{ln(1 \pm \epsilon).K} = \frac{ln(L)/K} { \left[ ln(1 \pm \epsilon) - ln(1) \right] / (\pm \epsilon) } = \frac{ ln(L)/K }{ ln'(t)|_{t = 1} } = \frac{ln(L)}{K} $$ This proves that the Quotient Function has an unique derivative in $(0,1)$. Now it should also be possible to devise a Taylor expansion around the attractor: $$ \frac{b}{a} \left( \frac{dx}{2^N} \right) = \frac{b}{a}(0) + \left[ \frac{b}{a} \right] \! '(0) \: \frac{dx}{2^N} + \: ... = 1 + \left[ \frac{b}{a} \right] \! '(0) \: \frac{dx}{2^N} + \: ... $$ Herewith we can write: $$ \left[ \frac{b}{a} \left( \frac{dx}{2^N} \right) \right]^{2^N} \approx \left( 1 + \left[ \frac{b}{a} \right] \! '(0) \: \frac{dx}{2^N} \right)^{2^N} $$ A relationship which will become better and better, as the grid becomes more and more refined. In the limiting case, of a "continuous" mesh, we find: $$ \frac{b}{a}(dx) = \lim_{N \rightarrow \infty} \left[ 1 + \left[ \frac{b}{a} \right] \! '(0) \: \frac{dx}{2^N} \right]^{2^N} = e^{\, \left[ b/a \right]'(0) \: dx} $$ As far a we can see, no special meaning should be attached to the term $\left[ b/a \right] \! '(0)$. We found that it is equal to: $$ \left[ \frac{b}{a} \right] \! '(0) = \frac{ln(L)}{K} $$ But $L$ as well as $K$ can be anything, since we assumed that, for a certain mesh spacing $K$, there exists a starting point $L$ such that $b/a(K) = L$. If we simply put the factor equal to some arbitrary constant $P := ln(L)/K$, then: $$ \frac{b}{a}(dx) = e^{P.dx} = L^{dx/K} \EN \frac{a}{b}(dx) = e^{-P.dx} $$ And it is easily shown that known persistence properties for the off-diagonal quotients remain completely unaffected: $$ \left( \left[ \frac{b}{a} \right] \! (dx) \right)^2 = \left( e^{P.dx} \right)^2 = e^{P.(2.dx)} = \left[ \frac{b}{a} \right] \! (2.dx) $$ $$ \left( \left[ \frac{b}{a} \right] \! (dx) \right)^{1/2} = \left( e^{P.dx} \right)^{1/2} = e^{P.(dx/2)} = \left[ \frac{b}{a} \right] \! (dx/2) $$ Now, indeed, we find the desired generalization of these properties: $$ \frac{b}{a} \: (p.dx) = e^{P.p.dx} = \left[ e^{P.dx} \right]^p = \left[ \frac{b}{a} \: (dx) \right]^p \quad \mbox{for any real} \; p $$