NO two clocks?
Until now, we have assumed that the following hypothesis holds water:
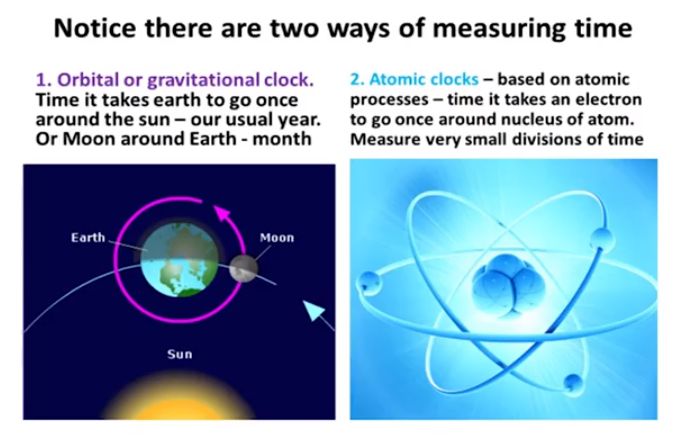
So there would exist two types of clocks: gravitational clocks and atomic clocks. Within the framework of
Halton Arp's theory of increasing elementary particle mass,
it has been previously argued that these two types of clocks are going to run
out of sync in due time. To be precise:
$$
\frac{dt}{dT} = \frac{T_0-A}{T-A} \quad \Longrightarrow \quad t-t_0=(T_0-A)\ln\left(\frac{T-A}{T_0-A}\right)
$$
Where $dt$ and $dT$ are the infinitesimal units of atomic time and gravitational time respectively; $T$ is gravitational time; $T_0=t_0$
is gravitational/atomic reference time, which is the "nowadays" timestamp and $A$ is the gravitational timestamp corresponding with the
beginning, at the time when mass is created out of nothingness.
A very much alike
theory has been proposed by Barry Settterfield but the latter has been
proved wrong. Obviously that theory has been developed to dishonestly save the cabbage (evolutionist view)
and the goat (creationist view): with wrong mathematics.
However, we are not certain anymore about the correctness or our own view
as well. The reason is that the two clocks hypothesis leads to doubtful consequences. Such as a (sidereal)
pendulum which is measurably going to run out
of sync when compared with "normal" atomic time. Such as a Sidereal year
which is going to last two days longer nowadays as expected. Worse: as NOT observed. Therefore we are going to search for reasons
why clocks - even in a increasing elementary particle mass scenario - shall stay in tune with each other.
Why should biblical chronology be different from secular chronology anyway?
Intrinsic redshift
The Rydberg formula is given by:
$$
\frac{1}{\lambda_0} = R_0 \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right)
$$
With somewhat different notation as in the references, for some good reasons.
Here $n_1$ and $n_2$ are any two different positive integers and $\lambda_0$
is the wavelength (in vacuum) of the emitted or absorbed light.
The Rydberg constant
$R_0$, with $m_0$ the electron rest mass, $h$ the Planck constant, $c$ the speed of light
and $\alpha$ the fine-structure constant, is given by:
$$
R_0 = \frac{m_0 c^2}{h c}\frac{\alpha^2}{2} =
1.097\;373\;156\;8539(55) \times 10^7 \,\text{m}^{-1}
$$
The fine-structure constant
$\alpha$, with $e$ elementary charge,
$\hbar = h/2\pi$ the reduced Planck constant, $\epsilon_0$
the electric permittivity of free space,
$\mu_0$ the magnetic permittivity of free space, is given by:
$$
\alpha = \frac{1}{4\pi\epsilon_0}\frac{e^2}{\hbar c} = \frac{\mu_0}{4 \pi} \frac{e^2 c}{\hbar}
\qquad \mbox{where} \qquad \alpha^{-1} \approx 137.035\,999\,139(31)
$$
Whatever the picture of the cosmos will be, everybody shall agree upon the fact that
what we see in distant space is actually "old" information that originated (light)years
ago, due to the speed of light which is known (or assumed) to be finite. Thus what we
in fact see is younger matter.
Now take a look again at the Rydberg constant. The only mass in there is the electron
rest mass $m_0$. Suppose that this rest mass has been different / smaller in the past,
say with a value $m$. Then we have for the Rydberg constant $R$ at that time:
$$
R = \frac{m c^2}{h c}\frac{\alpha^2}{2} =
\frac{m}{m_0} \frac{m_0 c^2}{h c}\frac{\alpha^2}{2} = \frac{m}{m_0} R_0
$$
And for the wavelengths at that time:
$$
\frac{1}{\lambda} = R \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right) = \frac{m}{m_0} R_0
\left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right) = \frac{m}{m_0} \frac{1}{\lambda_0}
\\ \Longrightarrow \quad \large \boxed{\lambda = \frac{m_0}{m} \lambda_0}
$$
Here $\lambda_0$ and $m_0$ are the values of wavelength and (electron rest) mass here and now.
Conclusion: wavelengths of electromagnetic radiation are inversely proportional to (varying)
elementary particle (rest) mass.
As for the atomic clock, associated with the above, with $c=$ light speed, $T=$ period of the clock:
$$
\lambda = c\,T \quad \Longrightarrow \quad \large \boxed{T = \frac{m_0}{m} T_0}
$$
It is noticed that the Rydberg constant is variable with atomic time, namely proportional with the
elementary particle mass, according to : $R/R_0 = m/m_0$ .
is approximately equal to the most probable distance between the nucleus and the electron in
a hydrogen atom in its ground state. It is given by:
$$
a_0 = \frac{4 \pi \varepsilon_0 \hbar^2}{m_0 e^2} = \frac{\hbar}{m_0\,c\,\alpha}
$$
with meaning of the constants as explained before. Suppose again that the elementary particle
(rest) mass (of the electron) has been different / smaller in the past, say with a value $m$.
Then we have for the Bohr radius $a$ at that time:
$$
a = \frac{\hbar}{m\,c\,\alpha} = \frac{m_0}{m}\frac{\hbar}{m_0\,c\,\alpha} \\ \Longrightarrow
\quad \large \boxed{a = \frac{m_0}{m} a_0}
$$
Here $a_0$ and $m_0$ are the values of the Bohr radius and (electron rest) mass here and now.
Conclusion: the Bohr radius is inversely proportional to (varying) elementary particle (rest) mass.
The Compton wavelength of a particle is equal to the wavelength of a photon whose energy is the same
as the mass of that particle. The standard Compton wavelength, $\lambda$, of a particle is given by:
$$
\lambda_0 = \frac{h}{m_0\,c}
$$
with meaning of the constants as explained before. Suppose again that the elementary particle
(rest) mass has been different / smaller in the past, say with a value $m$.
Then we have for the Compton wavelength $\lambda$ at that time:
$$
\lambda = \frac{h}{m\,c} = \frac{m_0}{m} \frac{h}{m_0\,c} \\ \Longrightarrow
\quad \large \boxed{\lambda = \frac{m_0}{m} \lambda_0}
$$
Conclusion: the Compton wavelength of an elementary particle is inversely proportional to its
(varying rest) mass.
The Planck mass is defined by:
$$
m = \sqrt{\frac{\hbar\,c}{G}} \approx 21.7651\,\mu g
$$
Herefrom it follows that:
$$
G = \frac{\hbar\,c}{m^2}
$$
Let's assume that Planck particles have
some physical significance. My own interpretation is as follows. Tiny black holes do not exist,
for the simple reason that singularities never really exist in physics. But it may be that they are
sort of upper/lower bound to the existence of real elementary particles, meaning for example that
particles heavier than Planck particles cannot come into existence.
With subscript $0$ for nowadays values and assuming a variable Planck mass, we then derive that the
Gravitational Constant may be variable as well:
$$
G_0 = \frac{\hbar\,c}{m_0^2} \quad \Longrightarrow \quad
\large \boxed{\frac{G}{G_0} = \left(\frac{m_0}{m}\right)^2}
$$
Conclusion: the Gravitational Constant may be inversely proportional to the square of (varying rest)
mass of elementary particles.
References:
Pendulum
This has consequences for gravitational clocks, such as a pendulum. The basic formula for the period $T$ of an (ideal) pendulum is, according to the Wikipedia
reference:
$$
T = 2\pi \sqrt{\frac{L}{g}}
$$
Where $g=$ gravitational acceleration
and $L=$ length of the pendulum. The length of a rod or a rope is built
from atoms. These atoms have sort of a Bohr radius. If the Bohr radius changes, then it may be expected
that the length of the rod or the rope is changing as well, inversely proportional to the (varying rest)
mass of the particles it is made from. All lengths $L$ in the preceding sections obey this law:
$$
\large \boxed{L = \frac{m_0}{m} L_0}
$$
And for the gravitational acceleration $g$ we have:
$$
g = \frac{G\,M}{R^2} = G_0\left(\frac{m_0}{m}\right)^2\times M_0\frac{m}{m_0}\times\left(\frac{m}{m_0}\right)^2/R_0^2
= g_0 \frac{m}{m_0} \\ \Longrightarrow \quad T = 2\pi \sqrt{\frac{L}{g}} = 2\pi \sqrt{\frac{L_0}{g_0}}\cdot\frac{m_0}{m}
= \frac{m_0}{m} T_0
$$
Conclusion: the ticks of a gravitational clock are inversely proportional to the varying elementary particles (rest)
mass.
Exactly as with atomic clocks. Thus there is no difference (anymore) between gravitational clocks and atomic
clocks.
