Latest revision 25-01-2020

index

C-decay data fit

So it seems we have rediscovered Barry Setterfield's (in)famous law of varying light speed, as described in chapter 3 of the book Cosmology and the Zero Point Energy. Formulated in our own terms it reads: $$ c=c_0\frac{T_0-A}{T-A} $$ Here $c=$ speed of light as measured with orbital time, $c_0 = 299\,792\,458\,m/s =$ reference lightspeed (constant by definition), $T=$ orbital time, $T_0=1983$ year = gravitational reference time (which is the "nowadays" timestamp), $A=$ gravitational timestamp corresponding with a beginning (Alpha), at the time when rest mass is created out of nothingness.
However, the document where it all started with is not a fat book, but the 1987 report The Atomic Constants, Light, and Time. It is an advantage that this report stands online. And it is formatted neatly in native HTML. Thanks to this a great deal of the work could be automated and data be extracted without too much effort. The only thing relevant for us, of course, is the relationship between orbital time (year) and lightspeed. The 1987 report has served as input for an aflezen.dpr program, resulting in 31 tables, not all of them useful for our purpose. Here are the relevant ones:

nr. Table name in 1987 document
1
 TABLE A
2 TABLE 1 - ROEMER METHOD VALUES
3 TABLE B
4 TABLE 3 - BRADLEY ABERRATION METHOD: PULKOVA VALUES MARKED *
5 TABLE 4 - TOOTH WHEEL EXPERIMENTAL VALUES
6 TABLE 5 - ROTATING MIRROR EXPERIMENTS
7 TABLE 6 - KERR CELL VALUES* OF C
8 TABLE 7 - RESULTS* BY SIX METHODS 1945-1960
9 TABLE 9 - C VALUES BY THE RATIO OF ESU/EMU
10 TABLE 10 - C VALUES BY WAVES ON WIRES
11 TABLE 11 - REFINED LIST OF C DATA (See Figs. II, III, IV)
12 TABLE 21 - COMPARISON OF CURVES FITTED TO ALL TABLE 11 DATA
13 TABLE 22 - RESULTS OF ANALYSIS OF SPEED OF LIGHT DATA

Problem description.
Let there be given a set of $N$ real-valued data points $(T_k,c_k)$. In addition, $c_0$ and $T_0$ are known fixed values. Find the (Least Squares) best fit of these points to the hyperbola $$ c = c_0\frac{T_0-A}{T-A} $$ The general form of the Least Squares data fit problem is: $$ \sum_k \left[\;F(T_k,c_k,A)\;\right]^2 = \mbox{minimum}(A) $$ Our purpose is to find $A$. The function $F(T,c,A)$ is not unique, thereby giving rise to several methods. What's worse: with (very) different outcomes for $A$. It should be noted that the actual problem is rather ill-conditioned, but I want to have results nevertheless.
Method 1. $$ F(T,c,A) = c(T-A)-c_0(T_0-A) \quad \Longrightarrow \\ \sum_k \left[c_k(T_k-A)-c_0(T_0-A)\right]^2 = \mbox{minimum}(A) $$ The minimum is found by differentiation and $dF/dA = 0$, giving: $$ A = \frac{\sum_k (T_kc_k-T_0c_0)(c_k-c_0)}{\sum_k(c_k-c_0)^2} $$ Method 2. $$ F(T,c,A) = A - \frac{Tc-T_0c_0}{c-c_0} \quad \Longrightarrow \\ \sum_k \left[A - \frac{T_kc_k-T_0c_0}{c_k-c_0}\right]^2 = \mbox{minimum}(A) $$ The minimum is found again by putting $dF/dA = 0$, giving: $$ A = \frac{1}{N} \sum_k \frac{T_kc_k-T_0c_0}{c_k-c_0} $$ Method 3. Without least squares: $$ \overline{T} = \frac{1}{N}\sum_k T_k \quad ; \quad \overline{c} = \frac{1}{N}\sum_k c_k \quad \Longrightarrow \\ A = \frac{\overline{T}.\overline{c}-T_0c_0}{\overline{c}-c_0} $$ There is no secret with the source code of the (Delphi Pascal) programs employed for the data fit:

Results for year of Creation $A$ (Alpha)

Leftmost in the table are simple plain text representations of tables in the 1987 document.
Colors in the graphs - rightmost in the table - are defined as follows. It is clear that only years B.C. are acceptable as a possible outcome.
Obviously, there are no positive year values for Let there be light.

table method 1 method 2 method 3 graph
1.txt -325,413 -1,423,711 -496,282 1.jpg
2.txt -13,394 -75,379 5,089 2.jpg
3.txt -90,126 -453,301 -128,157 3.jpg
4.txt -21,805 -38,506 -356,226 4.jpg
5.txt -1,101 -120,034 -10,792 5.jpg
6.txt 15,574 -790,987 204,518 6.jpg
7.txt 745,298 1,160,883 871,730 7.jpg
8.txt -1,448,385 10,066,734 -2,762,4247 8.jpg
9.txt 3,552 -75,689 4,561 9.jpg
10.txt 2,641 -1,133,758 327,940 10.jpg
11.txt -104,606 5,095,436 -297,469 11.jpg
12.txt -94,900 1,713,813 -158,783 12.jpg
13.txt -86,008 490,001 5,559 13.jpg

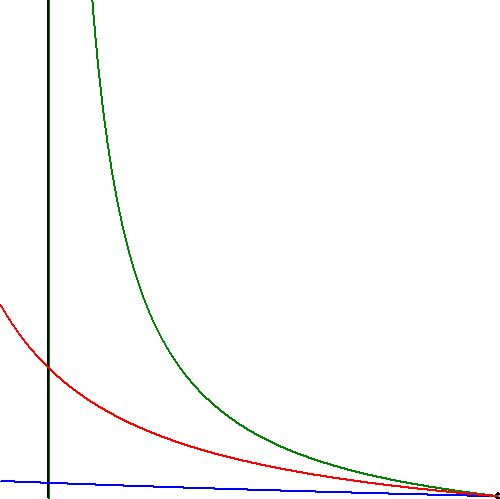
It is seen that there is an enormous spread in the results, which also becomes clear from the graph below.
The problem is extremely ill-conditioned, that's for sure; just look at the data that must do the job, almost invisible, rightmost in the picture.

The above results have been generated with $c = c_0.(T_0-A)/(T-A)$ as the basic template. At an earlier stage, we have solved a slightly more general problem, which has been published as a question at the Mathematics Stack Exchange platform, without significantly better results though: Error $\Delta A$ in Least Squares best fit of data to hyperbola $y=B/(x-A)$.