previous   overview   next

The Axiom of Specification

If $S$ is a set and $p(.)$ is an open sentence for the elements of $S$, then the collection of all elements $x\in S$ that satisfy $p(x)$ is a set too. It is denoted $\left\{x \in S : p(x)\right\}$ or $\left\{x \in S \,|\, p(x)\right\}$.
With other words: for every set and every condition, there corresponds a set whose elements are exactly the same as those elements of the original set for which the condition is true.
A two-dimensional example is: $$ C = \left\{(x,y)\in\mathbb{R}^2 : x^2+y^2\lt 1\right\} $$ Which is the set of all points $(x,y)$ of the plane $\mathbb{R}^2$ inside a unit circle with midpoint at the origin.
Reality is a bit more complicated, though. Instead of the plane we have a computer screen with pixels $[i,j]$. Let the width of the screen in pixels be $W$ and the height of the screen in pixels be $H$. On the other hand we have our Euclidean plane (world) coordinates $(x,y)$. Let the minimum and maximum $x$-coordinates be $(\mbox{xmin},\mbox{xmax})$ and the minimum and maximum $y$-coordinates be $(\mbox{ymin},\mbox{ymax})$. What we need in the first place are functions that convert the world coordinates into pixel coordinates $(\mbox{x2i},\mbox{y2j})$ and the other way around $(\mbox{i2x},\mbox{j2y})$ : 
W := W-1 ; H := H-1;

function x2i(x : double) : integer;
begin
  x2i := Round((x-xmin)/(xmax-xmin)*W);
end;

function i2x(i : integer) : double;
begin
  i2x := xmin + i/W*(xmax-xmin);
end;

function y2j(y : double) : integer;
begin
  y2j := Round(H*(1-(y-ymin)/(ymax-ymin)));
end;

function j2y(j : integer) : double;
begin
  j2y := ymin + (H-j)/H*(ymax-ymin);
end;
Then the following program snippet is equivalent with the Axiom of Specification for the inside of a unit circle. Mind the (if then) statement and the (pixels $\to$ world) mapping. 
function C(x,y : double) : boolean;
begin
  C := sqr(x)+sqr(y) < 1;
end;

procedure tekenen;
var
  i,j,k : integer;
  p,q : double;
begin
{ Axiom of Specification }
  for j := 0 to H-1 do
  begin
    for i := 0 to W-1 do
    begin
      if C(i2x(i),j2y(j)) then
        Form1.Image1.Canvas.Pixels[i,j] := clRed;
    end;
  end;
end;
It is noticed that there is no other way within the context of Implementable Set Theory, because there are no other sets than bit patterns in computer memory. The latter in turn are equivalent to natural numbers. And that's all. Whatever. The output is something like this:

Another open sentence for the elements of our screen $\mathbb{R}^2$ - in world coordinates - can be defined. Is there any equation for triangle?. The answer is yes. So let's have a look at the inside $D(x,y)$ of an arbitrary triangle, with vertices $(x_1,y_1),(x_2,y_2),(x_3,y_3)$: 

function min(a,b,c : double) : double;
var
  m : double;
begin
  m := a;
  if b < a then m := b;
  if c < m then m := c;
  min := m;
end;

function D(x,y : double) : boolean;
var
  xi,eta,det : double;
begin
  det := (x2-x1)*(y3-y1)-(x3-x1)*(y2-y1);
  xi := ((y3-y1)*(x-x1)-(x3-x1)*(y-y1))/det;
  eta := ((x2-x1)*(y-y1)-(y2-y1)*(x-x1))/det;
  D := min(xi,eta,1-xi-eta) > 0;
end;
Or consider the open sentence for the elements of a half plane delimited by a line with support $(p_1,q_1),(p_2,q_2)$: 
function L(x,y : double) : boolean;
begin
  L := (q2-q1)*(x-p1)-(p2-p1)*(y-q1) < 0;
end;
And we can define an open sentence or rather another boolean function that combines the circle, the triangle and the half plane with a little bit of logic: 
function S(x,y : double) : boolean;
begin
  S := (C(x,y) or D(x,y)) and (not L(x,y));
end;
Then the output may have become something like this:

It is noticed that the above is more or less the two-dimensional equivalent of a technique in 3-D, which is known as Constructive Solid Geometry (CSG).
That being said, there is a far more systematic way of laying down the elementary pieces of the puzzle, namely as follows. \begin{eqnarray*} 000 : \quad & S_0 = \overline{C} \cap \overline{D} \cap \overline{L} \\ 001 : \quad & S_1 = \overline{C} \cap \overline{D} \cap L \\ 010 : \quad & S_2 = \overline{C} \cap D \cap \overline{L} \\ 011 : \quad & S_3 = \overline{C} \cap D \cap L \\ 100 : \quad & S_4 = C \cap \overline{D} \cap \overline{L} \\ 101 : \quad & S_5 = C \cap \overline{D} \cap L \\ 110 : \quad & S_6 = C \cap D \cap \overline{L} \\ 111 : \quad & S_7 = C \cap D \cap L \\ \end{eqnarray*} Here the overline denotes the complement of a set: outside instead of inside.
Expressed in terms of our favorite programming language: 
function MT(x,y : double) : boolean;
{
  Minterms
}
var
  S : boolean;
begin
  S := false;
  case keer of
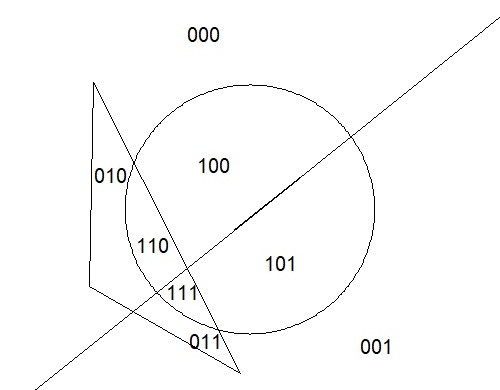
  0 : S := (not C(x,y)) and (not D(x,y)) and (not L(x,y)); { 000 }
  1 : S := (not C(x,y)) and (not D(x,y)) and      L(x,y) ; { 001 }
  2 : S := (not C(x,y)) and      D(x,y)  and (not L(x,y)); { 010 }
  3 : S := (not C(x,y)) and      D(x,y)  and      L(x,y) ; { 011 }
  4 : S :=      C(x,y)  and (not D(x,y)) and (not L(x,y)); { 100 }
  5 : S :=      C(x,y)  and (not D(x,y)) and      L(x,y) ; { 101 }
  6 : S :=      C(x,y)  and      D(x,y)  and (not L(x,y)); { 110 }
  7 : S :=      C(x,y)  and      D(x,y)  and      L(x,y) ; { 111 }
  end;
  MT := S;
end;
And here comes a vizualization of these elementary pieces of our puzzle:

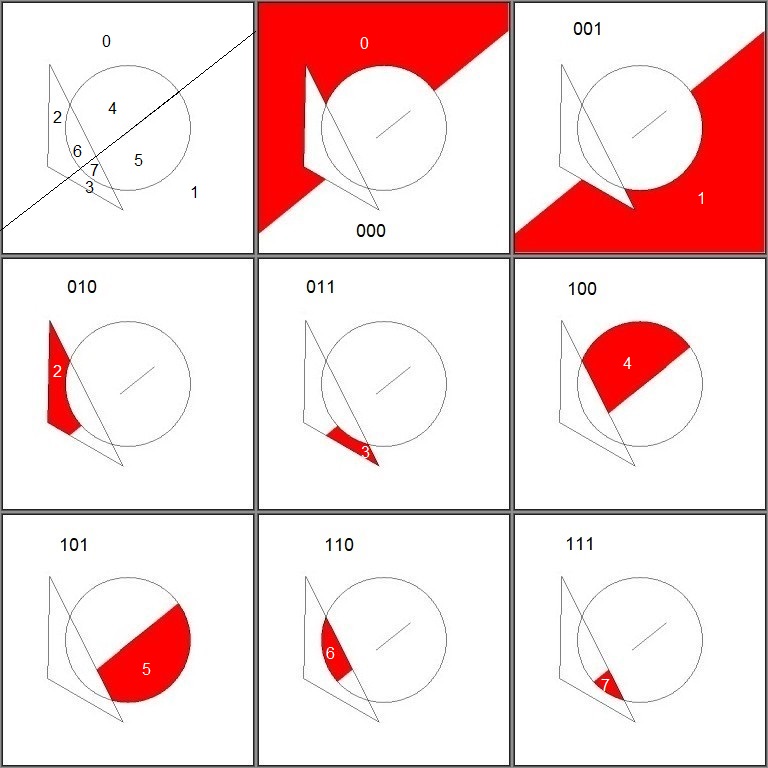
It is observed that the sets $S_k$ with $k=0,1, \cdots ,7$ - also called (equivalence) classes - form a partition of the computer screen / the (finite window) plane $\mathbb{R}^2$: $$ S_k \neq \emptyset $$ $$ ( S_i \neq S_j ) \Rightarrow (( S_i \cap S_j) = \emptyset ) $$ $$ \bigcup_k S_k = \mathbb{R}^2 $$ With the elements of the partition $\left\{S_k\right\}$, any other set in the plane can be composed by union, such as with the one in the second picture (repeated here for convenience): $$ S_{246} = S_2 \cup S_4 \cup S_6 $$
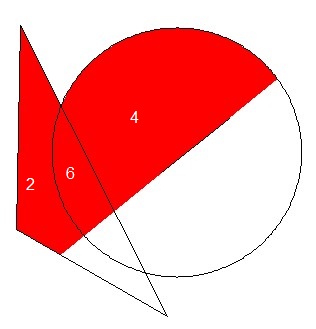
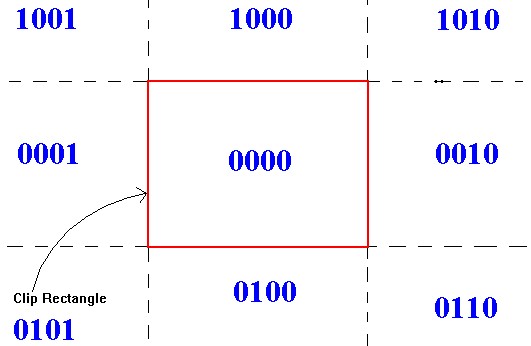
Quite a similar technique is employed with The Cohen-Sutherland Line-Clipping Algorithm: take a look at the Outcodes and compare them with the binary coding for the classes $S_k$ in our partition.

 

Another obvious similarity is found with Karnaugh maps. Copied without permission from a 1964 book on Boolean algebra by Graham Flegg:

 

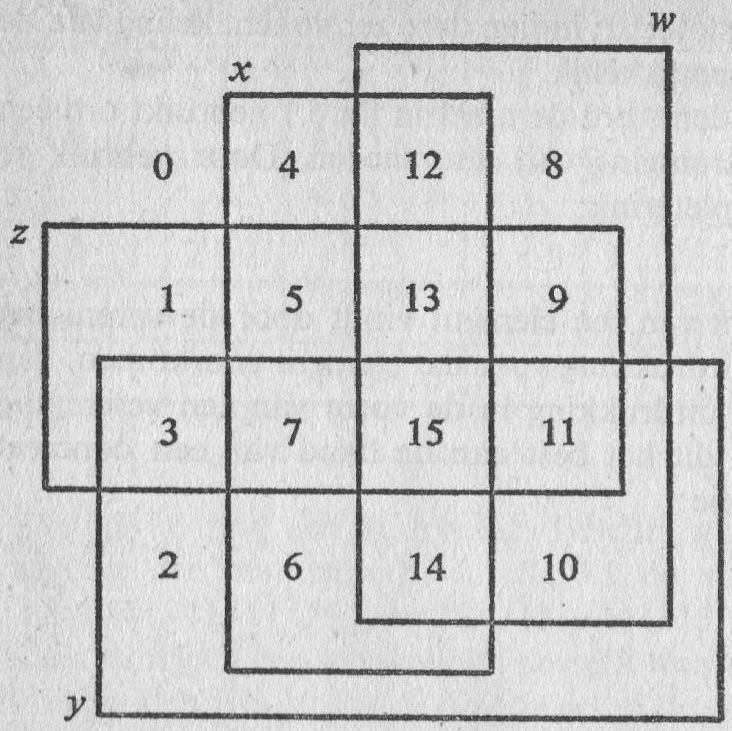
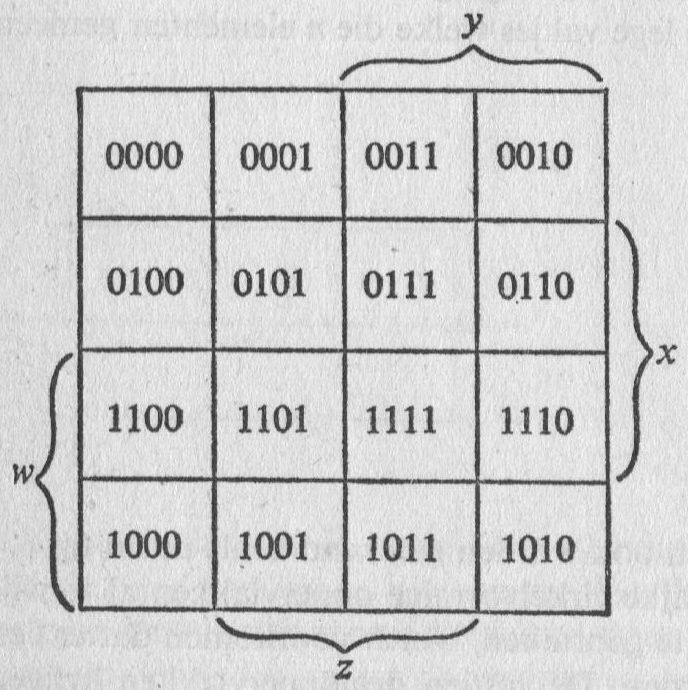
Also read my old musings about Members = Classes in an Elementary Partition.

So far so good, it seems. Further restriction of our thoughts reveals, however, that each of the above sets is merely a visualization of an open sentence. Thus the corresponding open sentence, also called predicate (in second order logic), or boolean function (in programming languages), is the essential thing and the set is just a picture of it. At best there is an equivalence relation between the sets and the predicates. Maybe the sets even should be replaced by their predicates. All this has already become clear by our programming efforts. Now let us put forward it formally: $$ \begin{eqnarray*} 0 = 000 : \quad & S_0(.) = & \neg C \wedge \neg D \wedge \neg L \\ 1 = 001 : \quad & S_1(.) = & \neg C \wedge \neg D \wedge \;\; L \\ 2 = 010 : \quad & S_2(.) = & \neg C \wedge \;\; D \wedge \neg L \\ 3 = 011 : \quad & S_3(.) = & \neg C \wedge \;\; D \wedge \;\; L \\ 4 = 100 : \quad & S_4(.) = & \;\; C \wedge \neg D \wedge \neg L \\ 5 = 101 : \quad & S_5(.) = & \;\; C \wedge \neg D \wedge \;\; L \\ 6 = 110 : \quad & S_6(.) = & \;\; C \wedge \;\; D \wedge \neg L \\ 7 = 111 : \quad & S_7(.) = & \;\; C \wedge \;\; D \wedge \;\; L \\ \end{eqnarray*} $$ We shall see that, with the elementary predicates (minterms) as members, there is a dual set theory.
Let each of the sets $S_k$ be defined as $S_k = \{ S_k(.) \}$ with $k=0,1, \cdots ,7\,$. Then we still have the following easy to prove properties: $$ S_k \neq \emptyset $$ $$ ( S_i \neq S_j ) \Rightarrow (( S_i \cap S_j) = \emptyset ) $$ $$ \bigcup_k S_k = U $$ Where $\emptyset$ is the empty set and $U$ is a (restricted) universe. Such is in concordance with: $$ ( S_i(.) \neq S_j(.) ) \Rightarrow (( S_i(.) \wedge S_j(.)) = \mbox{FALSE} ) \\ \bigvee_k S_k(.) = \mbox{TRUE} $$ With our example, at last: $$ \{ S_{246}(.) \} = \{ S_2(.) \vee S_4(.) \vee S_6(.) \} = \{ S_2(.)\} \cup \{ S_4(.)\} \cup \{ S_6(.)\} = \{S_2(.) , S_4(.) , S_6(.)\} = \{2,4,6\} $$ There is a landing on known territory if the story can be continued with: $$ \{2,4,6\} = 0101010 = 64+16+2 = 82 = \{\, \{\{\{\}\}\} , \{\{\{\{\}\}\}\} , \{\{\{\}\}\{\{\{\}\}\}\} \,\} $$ The above finally resolves my (very personal) problems with the so-called ZFC Killer Axiom.
In retrospect, it's very simple: members may be predicates. I have just mixed up the specifications with the sets that are constructed with them.