overzicht overview
Theorie van Bopp
In het hoofstuk Laplace en statistiek
hebben we ontmoet de volgende bewerker, die
tot effekt heeft dat een willekeurige funktie op zijn domein als het ware wordt
"uitgesmeerd", over een gebiedje ter grootte $ \sigma $:
$$ e^{ \frac{1}{2} \sigma^2 ( d/dx )^2 } $$
We hadden deze operator een sensor kunnen noemen. De gevoeligheid
van de sensor is omgekeerd evenredig met de spreiding $\sigma$ in de exponent.
Generalisatie van de sensor $S$ naar drie dimensies is rechttoe rechtaan:
$$ S = e^{ \frac{1}{2} \sigma^2 \nabla^2 } $$ Hierin is $ \nabla^2 =
\partial^2 / \partial x^2 + \partial^2 / \partial y^2 +
\partial^2 / \partial z^2 $.
Wanneer $S$ werkt op een funktie $f$, dan schrijven we: $\tilde{f}=S\,f$, en we
herkennen $\tilde{f}$ als de zin van $f$ (zodra $\sigma \rightarrow 0$).
Het heeft er de schijn van dat de sensor $S$ een zekere plaats toekomt binnen
het raamwerk van de klassieke elektrodynamika.
In [RPF] deel II lezen we over de
theorie van Bopp.
Nauw verwant hiermee
is de eigen theorie, die hieronder wordt gerepresenteerd. Wanneer men met het
elektron meebeweegt, dan wordt van alle elektromagnetische grootheden alleen
de elektrische komponent waargenomen. Inzoverre is de theorie dus algemeen.
We hebben gezien dat de veld-energie van een elektron, zoals die berekend wordt
volgens de klassieke elektrodynamika, uitkomt op een oneindige grootheid. Vraag
is nog steeds wat daarvan de oorzaak is. Om die vraag te kunnen beantwoorden
zullen we van begin af aan beter moeten kijken naar wat er in de werkelijkheid
gebeurt.
De veldsterkte van het elektron wordt \geintegreerd. Deze veldsterkte wordt op
haar beurt afgeleid van de wet van Coulomb, een wet die met grote experimentele
nauwkeurigheid is vastgesteld. Wat mankeert er dan aan? Wel, die experimentele
nauwkeurigheid! Het meten gaat altijd met behulp van een "voelspriet".
De gevoeligheid van zo'n meting is wel groot, maar ook weer niet zo groot dat
op de plaats van de puntlading zelf ooit een oneindig grote veldsterkte gemeten
zou kunnen worden. We hebben duidelijk vastgesteld dat het oneindige fysisch
niet bestaat.
Alles goed en wel, maar het is toch niet aannemelijk dat voor de veldsterkte
dan maar iets moet worden gesubstitueerd wat door ons stervelingen via de
de een of andere grove meetmethode wordt waargenomen? Dat zou toch een volkomen
willekeurige gang van zaken zijn? Inderdaad. Maar er is licht aan het eind van
de tunnel. Wordt er in de QuantumElektroDynamika immers niet gesproken over de
zelf-energie van het elektron? Dat is de energie die het elektron als het ware
van zichzelf opmeet. Alvorens deze energie met voortvarendheid te berekenen,
wat zou men denken van de "zelf-veldsterkte" van het elektron? Dat zou dan de
veldsterkte zijn die het elektron, met zijn eigen sensor, met een zeer grote
eigen gevoeligheid, van $ \hbar / m_0 c $ om zichzelf heen "waarneemt".
Op grond van het bovenstaande identificeren wij de gevoeligheid $\sigma$ van de
sensor $\exp(- \frac{1}{2} \sigma^2 \nabla^2) $ met de fundamentele quantummechanische
ruimtebegrenzing voor deeltjes in rust:
$$ \sigma = \frac{ \hbar }{ m_0 c } $$
Merk op dat, naarmate de deeltjes groter worden, de rustmassa evenredig groter
wordt, de spreiding $\sigma$ dus kleiner, en de operator $S$ steeds meer gaat
lijken op convolutie met een zeer steile piek: $$ \lim_{\sigma \rightarrow 0}
\frac{1}{ \sigma \sqrt{2\pi} } e^{\, -t^2 / 2\sigma^2 } = \delta (t) $$
Voor klassieke deeltjes is dus een met onnauwkeurigheid bewerkte golffunktie of
veldsterkte of elke andere grootheid gelijk aan zichzelf: $S \Psi = \Psi$, een
gevolg van de diafragma-eigenschap voor delta-funkties.
De veldsterkte voor een puntlading is $E = q/(4\pi\epsilon_0 r^2) $. We kunnen
nu het een en ander echt uitwerken. Een eerste aanzet luidt als volgt:
$ \tilde{E}(x,y,z) = $ $$ \left( \frac{1}{ \sigma \sqrt{2\pi} } \right)^3
\iiint \frac{q}{4 \pi \epsilon_0 ( \xi^2 + \eta^2 + \zeta^2 ) } \,
e^{\, - [ (\xi - x)^2 + (\eta - y)^2 + (\zeta - z)^2 ] / 2\sigma^2 }
\; d\xi d\eta d\zeta $$
Het lijkt interessant om eerst een speciaal geval te onderzoeken, namelijk de
waarde van $\tilde{E}$ in de oorsprong: $\tilde{E}(0,0,0)$.
De ruimte-integraal kan dan worden uitgerekend met behulp van bolschillen:
$$ \tilde{E}(r=0) \quad = \quad \left( \frac{1}{ \sigma \sqrt{2\pi} } \right)^3
\int_0^\infty \, \frac{q}{4 \pi \epsilon_0 r^2} e^{ - r^2 / 2 \sigma^2 } \,
4 \pi r^2 dr = $$
$$ \left( \frac{1}{ \sigma \sqrt{2\pi} } \right)^3 \frac{q}{\epsilon_0}
\int_0^\infty e^{- r^2 / 2 \sigma^2 } d r =
\left( \frac{1}{ \sigma \sqrt{2\pi} } \right)^3 \frac{q}{\epsilon_0}
\frac{1}{2} \sigma \sqrt{2\pi} = \frac{q}{4 \pi \epsilon_0 \sigma^2 }
= E(\sigma) $$
Dit is een fraaie uitkomst. Wanneer men de veldsterkte $E(r)$ korrigeert voor
de eindige afmetingen van het elektron, en vervolgens de waarde bepaalt in de
oorsprong, dan is het alsof men de "exakte" veldsterkte bepaalt op de rand van
het "harde bolletje" met straal $\sigma$ dat elektron heet.
De funktie $\tilde{E}$ is bolsymmetrisch om de oorsprong. Het is dus voldoende
de gemeten veldsterkte in \een\ richting, bijvoorbeeld de x-as, te bestuderen.
Om deze as kan men cylinder co\"ordinaten invoeren: $ \eta^2+\zeta^2 = r^2 $
en $ d\eta d\zeta = 2 \pi r \, dr $. Zonder beperking van de algemeenheid is
dan: $$ \tilde{E} = \left( \frac{1}{ \sigma \sqrt{2\pi} } \right)^3
\int_{-\infty}^{+\infty} e^{ - (x-\xi)^2 / 2 \sigma^2 } \left[
\int_0^\infty \, \frac{q}{4 \pi \epsilon_0 (\xi^2 + r^2) }
e^{ - r^2 / 2 \sigma^2 } \, 2 \pi r \, dr \right] d \xi $$
Het is zinvol om dimensieloze grootheden in te voeren: deel de lengtematen $x,
\xi, r $ door de elementaire afstand $\sigma$. Dan komt er na vereenvoudiging:
$$ \tilde{E} = \frac{q}{4 \pi \epsilon_0 \sigma^2} \frac{1}{2 \sqrt{2 \pi}}
\int_{-\infty}^{+\infty} e^{ - \frac{1}{2} (x-\xi)^2 } \left[
\int_0^\infty \, \frac{ e^{ - \frac{1}{2} r^2 } }{ r^2 + \xi^2 } \, dr^2
\right] d \xi $$
De integraal tussen vierkante haken is, via $t = \frac{1}{2} ( r^2 + \xi^2 ) $,
equivalent met:
$$ e^{\frac{1}{2} \xi^2} \int_{\frac{1}{2} \xi^2}^\infty \frac{ e^{- t} }{t} dt =
- e^{\frac{1}{2} \xi^2} \int_{-\infty}^{-\frac{1}{2}\xi^2} \frac{ e^{\,t}}{t} dt $$
De laatste integraal is een oude bekende, waarvan we inmiddels dus weten dat
zij niet analytisch te berekenen is. Het is namelijk weer de "exponenti\"ele
integraal", gedefinieerd als: $ Ei(x) = \int_{-\infty}^x \exp(t)/t \, dt $.
Omdat een formule voor de eigen-veldsterkte van het elektron blijkbaar niet te
verkrijgen is in gesloten vorm, is de enige weg die ons nu nog openstaat een
numerieke benadering. We gaan hiertoe uit van de volgende expressie, welke uit
het bovenstaande kan worden afgeleid:
$$ 2 \sqrt{ 2\pi } \, \tilde{E}(x) / E(\sigma) = e^{-\frac{1}{2} x^2}
\int_0^{\infty} \left( e^{x\xi} + e^{-x\xi} \right) \left[
- Ei( - \frac{1}{2} \xi^2 ) \right] d \xi $$
Natuurlijk kunnen we in de computer geen getallen $[ -\infty, +\infty ]$ kwijt.
We nemen in plaats daarvan een redelijk groot "betrouwbaarheids"interval, zeg
van de orde $6 \sigma$ (zie Statistiek). Funkties worden binnen \een\ $\sigma$
benaderd met een stuk of wat stappen, zeg $30$. We berekenen in zo'n 40 punten
van de x-richting door numerieke integraties de funktiewaarde $\tilde{E}(x)$,
en plotten het resultaat op het scherm. Volgt hier de listing van het BASIC
programma dat bij dit probleem behoort:
10 REM Eigen Veldsterkte van het Elektron
20 REM ==================================
30 REM Exponentiele integraal -Ei(-x^2/2):
40 RM=6 : KR=30 : DR=1/KR : LR=KR*RM
50 DIM EI(LR) : G=0 : EI(LR)=G : T=-.5*RM^2
60 FOR K=1 TO LR-1 : R=-RM+K*DR : TV=T : T=-.5*R^2
70 DT=T-TV : Y=-SQR(T*TV) : REM Meetkundig gemiddelde
80 G=G+EXP(Y)/Y*DT : EI(LR-K)=-G : NEXT K
110 REM Raster tekenen:
120 SCREEN(1) : CLS : COLOR 0,1 : SC=39
130 FOR I=1 TO 6 : Y=199-(I-1)*SC
140 LINE(0,Y)-(319,Y),1 : NEXT I
150 FOR I=1 TO 9 : X=(I-1)*SC
160 LINE(X,0)-(X,199),1 : NEXT I
175 PI=4*ATN(1) : VEEL=2*SQR(2*PI)
180 REM Laplace integraal van -Ei(-x^2/2):
185 XM=8 : KX=5 : DX=1/KX : LX=KX*XM
190 XV=0 : GV=VEEL : VV=VEEL
210 FOR I=1 TO LX : X=(I-1)*DX
225 FOR K=1 TO LR : R=K*DR
230 T=(EXP(R*X)+EXP(-R*X))*EI(K)
235 IF K=1 THEN G=.5*T*DR
240 G=G+T*DR : NEXT K : G=EXP(-X^2/2)*G
250 REM Klassieke & numerieke oplossing:
260 IF I<=KX THEN V=VEEL
270 IF I>KX THEN V=VEEL/X^2
280 LINE (SC*XV,199-SC*VV)-(SC*X,199-SC*V),2
290 LINE (SC*XV,199-SC*GV)-(SC*X,199-SC*G),3
300 XV=X : GV=G : VV=V : NEXT I
320 IF INKEY$="" THEN 320 ELSE END
In verband hiermee een vraag op het Mathematics forum:
Integral of exponential integral .
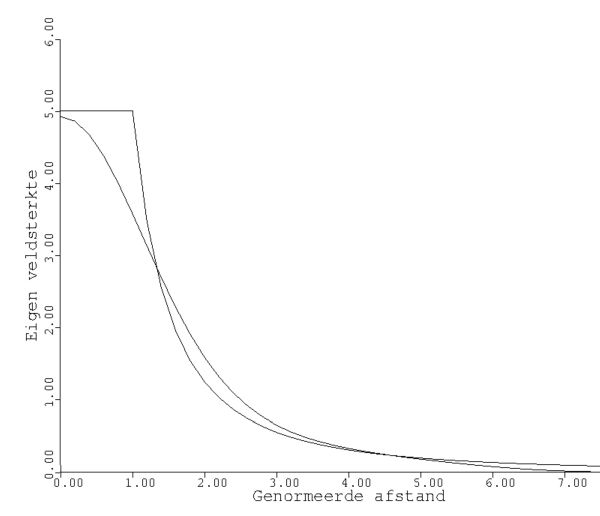
De grafiek is een weergave van de veldsterkte van het elektron, zoals die bij
benadering zou worden waargenomen met de grootste eigen gevoeligheid die door
de natuur kan worden opgebracht. Het resultaat van ons computerprogramma wordt
onnauwkeuriger naarmate men zich verder van de oorsprong verwijdert.
Op grond van analytische argumenten (uit de Statistiek) kan men echter inzien
dat de veldsterkte keurig de klassieke waarde benadert voor $ r \gg \sigma $.
Het resultaat van een waarneming met sensor $S$ van een gemeten funktie
$g(x,y,z)$ is in het algemeen een convolutie-integraal: $$ \tilde{g} =
\iiint f(\xi,\eta,\zeta) g(x-\xi,y-\eta,z-\zeta) d\xi d\eta d\zeta $$
Hierin is $f$ de sensor-funktie en $g$ de gemeten funktie.
Ontwikkel $g$ in een Taylor reeks om $(\xi,\eta,\zeta)=(0,0,0)$:
$$ g(x-\xi,y-\eta,z-\zeta) \; \approx \; g(x,y,z) $$
$$ - \xi \frac{\partial g}{\partial x} - \eta \frac{\partial g}{\partial y} - \zeta \frac{\partial g}{\partial z}$$
$$ + \frac{1}{2} \xi^2 \frac{\partial^2 g}{\partial x^2} + \frac{1}{2} \eta^2 \frac{\partial^2 g}{\partial y^2}
+ \frac{1}{2} \zeta^2 \frac{\partial^2 g}{\partial z^2}$$
$$ + \xi\eta \frac{\partial^2 g}{\partial x \partial y} + \eta\zeta \frac{\partial^2 g}{\partial y \partial z}
+ \zeta\xi \frac{\partial^2 g}{\partial z \partial x}$$
In deze uitdrukking hangen de \partiele\ differentiaal \quotienten\ niet langer
af van $(\xi,\eta,\zeta)$ omdat ze berekend zijn voor
$(\xi,\eta,\zeta)=(0,0,0)$. Zodat de convolutie-integraal ten naaste bij
gelijk wordt aan:
$$ g(x,y,z) \iiint \, f \, d\xi d\eta d\zeta $$ $$ \, - \, \frac{\partial g}{\partial x}
\iiint \xi \, f \, d\xi d\eta d\zeta \, - \, \frac{\partial g}{\partial y}
\iiint \eta \, f \, d\xi d\eta d\zeta \, - \, \frac{\partial g}{\partial z}
\iiint \zeta \, f \, d\xi d\eta d\zeta \; + $$ $$
\frac{1}{2} \frac{\partial^2 g}{\partial x^2}\iiint \xi^2 \, f \, d\xi d\eta d\zeta \, + \,
\frac{1}{2} \frac{\partial^2 g}{\partial y^2}\iiint \eta^2 \, f \, d\xi d\eta d\zeta \, + \,
\frac{1}{2} \frac{\partial^2 g}{\partial z^2}\iiint \zeta^2\, f \, d\xi d\eta d\zeta + $$
$$ \frac{\partial^2 g}{\partial x \partial y}\iiint \xi \eta \, f \, d\xi d\eta d\zeta \, + \,
\frac{\partial^2 g}{\partial y \partial z}\iiint \eta \zeta \, f \, d\xi d\eta d\zeta \, + \,
\frac{\partial^2 g}{\partial z \partial x}\iiint \zeta \xi \, f \, d\xi d\eta d\zeta $$
De eerste integraal is per definitie gelijk aan $1$. De volgende 3 integralen
zijn gelijk aan de verwachtingswaarde van de sensor-funktie, en daarom gelijk
aan $0$. De volgende 3 integralen zijn gelijk aan de spreidingen van de
sensor-funktie in de diverse coordinaat-richtingen. De laatste 3 integralen
tenslotte zijn nul. Dus: $$ \tilde{g} \approx
g + \frac{1}{2} \sigma_x^2 \frac{\partial^2 g}{\partial x^2} + \frac{1}{2} \sigma_y^2 \frac{\partial^2 g}{\partial y^2}
+ \frac{1}{2} \sigma_z^2 \frac{\partial^2 g}{\partial y^2} = g + \frac{1}{2} \sigma^2 \nabla^2 g $$
Een asymptotische benadering voor grote afstanden, die ook te vinden is
in menig boek over Statistiek [SC].
Toegepast op de veldsterkte rondom het elektron:
$$ \nabla^2 \frac{1}{r^2} =
\frac{1}{r} \frac{\partial^2}{\partial r^2} r \frac{1}{r^2} = \frac{2}{r^4} $$
En dus:
$$ \tilde{E} \approx E \left( 1 + \frac{\sigma^2}{r^2} \right) \qquad \mbox{ (veraf) } $$
De gevonden uitdrukking is een goede benadering voor de veldsterkte op redelijke
tot grote afstand van de puntlading. Men ziet hoe de korrektie op de klassieke
veldsterkte snel afneemt tot nul. We vinden een veldsterkte $\tilde{E}(x,y,z)$
die voor punten "ver" van de oorsprong veel gelijkenis vertoont met de klassieke
veldsterkte $E(x,y,z)$.
Houdt men vast aan een waarde $ \hbar / m_0 c $ voor de onnauwkeurigheid in de
positie van het elektron, dan is het elektromagnetische aandeel in de massa van
het elektron slechts een fraktie van het totaal: in de orde van grootte van de
fijnstruktuur-konstante ofwel $ 1/137$ (: zie appendix "Natuurkonstanten"). Dit
resultaat komt niet geheel onverwacht [RPF].
Het blijkt dat we de bij de operator $S$ behorende exponent ook tegenkomen in
het linkerlid van de Schrödinger vergelijking, mits we even de moeite nemen
om de laatste dimensieloos te maken. We schrijven iets anders dan gewoonlijk:
$$ \left[ \frac { E }{ m_0 c^2 }
+ \frac{1}{2} \left( \frac{\hbar}{m_0 c} \right)^2 \nabla^2 \right] \Psi
= \frac{ V }{ m_0 c^2 } \Psi $$
Blijkbaar is de (operator voor) kinetische energie gedeeld door rustenergie
gerelateerd aan het "volume" dat een "elementair deeltje" in de ruimte inneemt.
Wanneer de potentiaal $V$ gelijk aan nul is, dan is de term $E / (m_0 c^2)$
gelijk aan \een. Links van het gelijkteken staan dan de eerste twee termen van
de (Taylor)reeksontwikkeling voor $S$, ook wel bekend als "de infinitesimale
transformatie" (: Lie groepen) behorend bij $\exp(\frac{1}{2} \sigma^2 \nabla^2 )$.
