overzicht overview
Verenigde diffusie
De Numerieke Analyse is de Assepoester van de Wiskunde, goed om iedere keer het
zware werk op te knappen. De heel aparte schoonheid van de Numerieke Analyse
wordt niet alleen niet ingezien, maar vooral ook niet gewild. Stiefmoederlijk
behandeld, tot op de dag van vandaag, dient zij zich te voegen naar de Banach-
en Sobolev-ruimten van de funktionaal-analyse. Haar tegenstroom schema's worden
van onnauwkeurigheid verdacht, en haar beste elementen treft het verwijt dat ze
niet "conform" zijn. Door belachelijke bovengrenzen voor de nauwkeurigheid van
numerieke oplossingen te suggereren houdt men de vermeende superioriteit van de
klassieke analyse in stand. Zo Banach- en Sobolov-ruimten al iets van uitstaans
hebben met de Numerieke Wiskunde, leven zij op veel te grote voet. Het elegante
glazen muiltje zal deze stiefzusters vast niet passen.
Wat het fysische verschijnsel "diffusie" betreft zijn de controverses heel wat
minder uitgesproken dan bij konvektie. Maar het is goed ons standpunt nog eens
te herhalen:
De vraag is niet of het numerieke schema de Laplace-vergelijking oplost.
De vraag is of het numerieke schema het fysische verschijnsel diffusie afdoende
beschrijft, en of er een onderling verband is tussen de verschillende
benaderingen om dit te doen, inklusief de analytische.
Hiermee wil ik nogmaals benadrukken dat de klassieke en de numerieke analyse
gelijkwaardige wiskundige benaderingen zijn, en dat het belangrijk is er
van uit te gaan dat de numerieke benadering evenzeer vrij is van willekeur als
de klassieke analyse. We zullen behandelen een zogenaamde Unificatie Stelling,
van toepassing op een eindige Volumen (differentie) methode aan de ene kant, en
een eindige Elementen methode aan de andere kant. Beide numerieke methoden gaan
gaan uit van de volgende partiële differentiaal-vergelijking (PDV), indien we
ons (in dit boek) beperken tot het twee-dimensionale geval:
$$
\frac{\partial Q_x}{\partial x} + \frac{\partial Q_y}{\partial y} = 0
$$
Hierin zijn $(x,y) = $ globale coördinaten . Een mogelijke interpretatie van
de vektor $ (Q_x,Q_y) $ is een warmtestroom. De differentiaal-vergelijking
drukt dan behoud van warmte uit. In het geval van diffusie, beter bekend als
warmtegeleiding, hangen de warmtestromen samen met de temperatuur volgens:
$$
Q_x = \lambda \frac{\partial T}{\partial x} \qquad
\qquad Q_y = \lambda \frac{\partial T}{\partial y}
$$
Zodat de uiteindelijke differentiaal-vergelijking voor de temperatuur niet van
de eerste maar van de tweede orde is. Teneinde nu de PDV geschikt te maken voor
numerieke benadering, wordt er een integratie-procedure ingezet. Reeds op dit
punt is er een splitsing in twee wegen.
Bij de eindige elementen benadering wordt de differentiaal-vergelijking eerst
vermenigvuldigd met een willekeurige (test)funktie en vervolgens geïntegreerd
over het rekendomein. Noem de testfunktie $f$, dan:
$$
\iint f . \left[ \frac{\partial Q_x}{\partial x}
+ \frac{\partial Q_y}{\partial y} \right] \, dx dy = 0
$$
Het is in te zien dat deze integraal-formulering volkomen gelijkwaardig is met
de oorspronkelijke differentiaal-vergelijking. Dit zit 'm in het gegeven dat de
testfunktie $f$ willekeurig is.
Partieel integreren, of toepassen van de stelling van Green, dat is hetzelfde,
resulteert in een uitdrukking waar lijn-integralen (over randen) in voorkomen,
aangevuld met de volgende hoofdterm:
$$
- \iint \left[ \frac{\partial f}{\partial x}.Q_x
+ \frac{\partial f}{\partial y}.Q_y \right] \, dx dy
$$
Let op het minteken. Het hiermee behaalde voordeel is een orde-reductie van het
probleem. Immers de integrand bevat nu neacuteog uitsluitend partiële afgeleiden
van de eerste orde. Vervolgens wordt het rekendomein opgesplitst in elementen,
en daarmee ook de integraal, in bijdragen over de afzonderlijke elementen $E$:
$$
- \sum_E \iint \left[ \frac{\partial f}{\partial x}.Q_x
+ \frac{\partial f}{\partial y}.Q_y \right] \, dx dy
$$
Het simpelste eindige element in twee dimensies is de driehoek: zie de appendix
"DriehoeksAlgebra". Essentieel is de Differentiatie Matrix [ZJ],
waarmee partiële afgeleiden op een driehoek kunnen worden gediskretiseerd:
$$
\Delta \left[ \begin{array}{c} \partial f/\partial x \\ \partial f/\partial y \end{array} \right] =
\left[ \begin{array}{ccc} +(y_2 - y_3) & +(y_3 - y_1) & +(y_1 - y_2) \\
-(x_2 - x_3) & -(x_3 - x_1) & -(x_1 - x_2) \end{array}
\right] \left[ \begin{array}{c} f_1 \\ f_2 \\ f_3 \end{array} \right]
$$
In te zien is dat $\partial f/\partial x$ en $\partial f/\partial y$ konstant zijn, dat wil zeggen niet
meer in waarde variëren over het element. Aangezien bij diffusie ook $Q_x$ en
$Q_y$ partiële afgeleiden zijn, zijn ook deze konstant. Hiermee is de eindige
elementen formulering voor één driehoek gelijk aan:
$$
- \left[ \frac{\partial f}{\partial x}.Q_x +
\frac{\partial f}{\partial y}.Q_y \right] \iint dx dy =
- \left[ \frac{\partial f}{\partial x}.Q_x + \frac{\partial f}{\partial y}.Q_y \right] \Delta/2
$$
De resterende integraal is namelijk gelijk aan de oppervlakte van de driehoek.
De differentiatie matrix toepassend, vinden we:
$$
= - \frac{1}{2} \left[ \begin{array}{ccc} f_1 & f_2 & f_3 \end{array} \right]
\left[ \begin{array}{cc} y_2 - y_3 & x_3 - x_2 \\
y_3 - y_1 & x_1 - x_3 \\
y_1 - y_2 & x_2 - x_1 \end{array} \right]
\left[ \begin{array}{c} Q_x \\ Q_y \end{array} \right] =
$$ $$
= \frac{1}{2} \left[ \begin{array}{ccc} f_1 & f_2 & f_3 \end{array} \right]
\left[ \begin{array}{c} (y_3 - y_2) Q_x - (x_3 - x_2) Q_y \\
(y_1 - y_3) Q_x - (x_1 - x_3) Q_y \\
(y_2 - y_1) Q_x - (x_2 - x_1) Q_y \end{array} \right]
$$
We willen echter het eindige elementen domein niet in driehoeken opdelen maar
in vierhoeken. Nu kan een vierhoek op zijn beurt toch weer worden opgedeeld in
driehoeken, en wel op twee manieren:
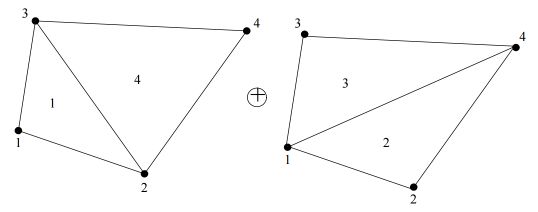
We willen bovendien een konfiguratie waarbij alle hoekpunten een gelijkwaardige
rol spelen. We zullen daarom alle 4 de driehoeken meenemen in onze formulering.
Het komt erop neer dat we in het resultaat hierboven de volgende permutatie van
knooppunts-nummers toepassen:
1 2 3 2 4 1 3 1 4 4 3 2
Tegelijkertijd geven we een aanduiding op welke driehoek gediskretiseerd wordt,
als boven-index (let op: geen macht!) bij de $(Q_x,Q_y)$ waarden. Alle vier de
bijdragen over de driehoeken worden gesommeerd (en nogmaals gehalveerd):
$$
\frac{1}{4} \left[ \begin{array}{ccc} f_1 & f_2 & f_3 \end{array} \right]
\left[ \begin{array}{c} (y_3 - y_2) Q^1_x - (x_3 - x_2) Q^1_y \\
(y_1 - y_3) Q^1_x - (x_1 - x_3) Q^1_y \\
(y_2 - y_1) Q^1_x - (x_2 - x_1) Q^1_y
\end{array} \right] +
$$ $$
\frac{1}{4} \left[ \begin{array}{ccc} f_2 & f_4 & f_1 \end{array} \right]
\left[ \begin{array}{c} (y_1 - y_4) Q^2_x - (x_1 - x_4) Q^2_y \\
(y_2 - y_1) Q^2_x - (x_2 - x_1) Q^2_y \\
(y_4 - y_2) Q^2_x - (x_4 - x_2) Q^2_y
\end{array} \right] +
$$ $$
\frac{1}{4} \left[ \begin{array}{ccc} f_3 & f_1 & f_4 \end{array} \right]
\left[ \begin{array}{c} (y_4 - y_1) Q^3_x - (x_4 - x_1) Q^3_y \\
(y_3 - y_4) Q^3_x - (x_3 - x_4) Q^3_y \\
(y_1 - y_3) Q^3_x - (x_1 - x_3) Q^3_y
\end{array} \right] +
$$ $$
\frac{1}{4} \left[ \begin{array}{ccc} f_4 & f_3 & f_2 \end{array} \right]
\left[ \begin{array}{c} (y_2 - y_3) Q^4_x - (x_2 - x_3) Q^4_y \\
(y_4 - y_2) Q^4_x - (x_4 - x_2) Q^4_y \\
(y_3 - y_4) Q^4_x - (x_3 - x_4) Q^4_y
\end{array} \right]
$$
Hier zit meer achter. Een andere manier om een formulering te bekomen waarbij
op alle vier de deel-driehoeken van een vierhoek wordt gediskretiseerd is de
zogenaamde numerieke integratie [OC]. Hiertoe worden binnen de vierhoek
vier punten gekozen, de zogenaamde Gauss punten. Deze liggen normaal gesproken
op $(\xi,\eta) = 1/(2\sqrt{3})$. (Verwezen wordt naar de appendix "VierkantsAlgebra"
voor uitleg over $\xi$ en $\eta$.) Het opent mogelijkheden indien men
deze exakte ligging met een korrel zout neemt. De integratie-punten kunnen dan
bijvoorbeeld gelokaliseerd worden ter plaatse van de hoekpunten. In dit geval
blijkt de vierhoek zich te gedragen als het samenstel van de gedeeltelijk over
elkaar liggende driehoeken, zoals geschetst in bovenstaande figuur. Tevens is
nu duidelijk waar de gewichtsfaktor $1/4$ vandaan komt, en dat de grootheden
$Q^k$ niet alleen geassocieerd zijn met de driehoeken, maar evenzeer met de
hoekpunten van de oorspronkelijke vierhoek.
Papier is geduldig, maar teneinde het schrijfwerk wat te bekorten bedenken we
de volgende afkorting, een soort uitprodukt:
$$
r_{ij} \times Q_k = (y_i - y_j) Q^k_x - (x_i - x_j) Q^k_y
$$
De termen behorend bij $f_k, k=1 ... 4$ worden bij elkaar gezocht. Men ziet de
standaard eindige elementen assemblage procedure gedemonstreerd in het klein.
Immers, wat is een eindige elementen matrix anders dan een onvolledig stelsel
vergelijkingen? Men vindt:
$$
\frac{1}{4} \left[ \begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array} \right]
\left[ \begin{array}{c}
r_{32} \times Q_1 + r_{42} \times Q_2 + r_{34} \times Q_3 + 0 \\
r_{13} \times Q_1 + r_{14} \times Q_2 + 0 + r_{34} \times Q_4 \\
r_{21} \times Q_1 + 0 + r_{41} \times Q_3 + r_{42} \times Q_4 \\
0 + r_{21} \times Q_2 + r_{13} \times Q_3 + r_{23} \times Q_4
\end{array} \right]
$$
Gebruik achtereenvolgens:
$$
r_{23} = r_{34} + r_{42} \qquad r_{14} = r_{13} + r_{34} \qquad
r_{41} = r_{42} + r_{21} \qquad r_{23} = r_{21} + r_{13}
$$
Om het bovenstaande in een handzamer vorm te gieten:
$$
\left[ \begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array} \right]
\left[ \begin{array}{c}
\frac{1}{2} r_{42} \times \frac{1}{2} (Q_1+Q_2) + \frac{1}{2} r_{34} \times \frac{1}{2} (Q_1+Q_3) \\
\frac{1}{2} r_{13} \times \frac{1}{2} (Q_1+Q_2) + \frac{1}{2} r_{34} \times \frac{1}{2} (Q_2+Q_4) \\
\frac{1}{2} r_{21} \times \frac{1}{2} (Q_1+Q_3) + \frac{1}{2} r_{42} \times \frac{1}{2} (Q_3+Q_4) \\
\frac{1}{2} r_{21} \times \frac{1}{2} (Q_2+Q_4) + \frac{1}{2} r_{13} \times \frac{1}{2} (Q_3+Q_4)
\end{array} \right]
$$
Het is een gemeenplaats, maar toch. Een beeld zegt meer dan duizend woorden:
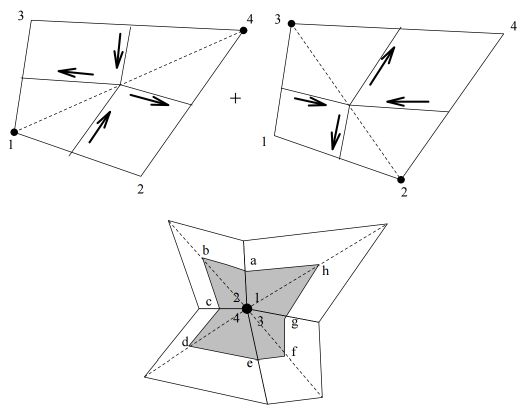
We zien dat de vier stukken van vergelijkingen overeenkomen met vier stukken
van kring-integralen, elk om één van de hoekpunten heen. Middens van zijden
worden verbonden door de lijnstukken waarover geïntegreerd wordt. Plaatselijk
is ook de warmtestroom een gemiddelde van knooppunts-waarden. Verplaatsen we nu
het gezichtspunt: concentreer de aandacht niet langer op het element maar op
een hoekpunt. In plaats van hoekpunten te rangschikken om een element heen,
rangschikt men elementen om een hoekpunt heen. Voegen we vervolgens alle
lijnstukken aaneen voor dat hoekpunt, dan blijkt de kring netjes gesloten te zijn.
Middens van zijden worden voorzien van etiketten $a,b,c,d,e,f,g,h$. Dan is het
resultaat, uitgedrukt in ons symbolisme:
$$
r_{ba} \times Q_a + r_{cb} \times Q_c + r_{dc} \times Q_c +
r_{ed} \times Q_e + r_{fe} \times Q_e + r_{gf} \times Q_g +
r_{hg} \times Q_g + r_{ah} \times Q_a
$$
Dit levert precies één vergelijking uit de eindige elementen systeem-matrix
of grote matrix. Het resultaat is dus nul (aangenomen dat ter plekke geen bron-
of rand-termen een rol spelen). De termen representeren samen, tegelijkertijd,
een diskretisatie van de volgende kring-integraal:
$$
\sum r \times Q = \oint Q_x dy - Q_y dx = 0
$$
Echter met behulp van de stelling van Green kan een kring-integraal ten allen
tijde worden omgezet in een oppervlakte-integraal, over het gearceerde gebied:
$$
\oint Q_x dy - Q_y dx =
\iint \left[ \frac{\partial Q_x}{\partial x} + \frac{\partial Q_y}{\partial y} \right] \, dx dy = 0
$$
Waar we nu op terecht zijn gekomen is een eindige Differentie methode, en wel
in het bijzonder een eindige volumen methode: integreer de wet van behoud van
warmte om een knooppunt heen, over een eindig volumen.
Dit is de grondslag voor diskretisatie met behulp van eindige volumen methoden.
Wanneer we het hele verhaal nu achterstevoren afdraaien, dan komen we weer uit
op een eindige elementen methode. Probeer namelijk vanuit de volumen-integraal
orde-reduktie tot stand te brengen. Dit kan worden bereikt door de integraal om
te zetten in een kring-integraal, met behulp van de stelling van Green. Kies de
omtrek van het integratie-gebied zodanig dat ... Enzovoort.
We hebben hiermee afgeleid een zogenaamde Unificatie Stelling:
Pas een eindige Elementen methode toe op een mesh van vierhoeken,
waarbij iedere vierhoek op de twee mogelijke manieren is opgedeeld in 4 elkaar
(dus) overlappende driehoeken. Dan is deze methode geheel en al equivalent met
een eindige Differentie (volumen) methode.
Merk op dat het geheel van toepassing is op kromlijnige rasters. Voor een wat
andere benadering is gekozen in [FTP], waar eerst wordt getransformeerd
naar een eindige differentie raster van vierkanten. Dit zou geen invloed mogen
hebben op het eindresultaat. Het is nu wel duidelijker dat de eindige volumes,
bij de onderhavige methode, niet netjes op elkaar aansluiten.
Een
Unifikatie Stelling zoals hierboven heeft nog al wat praktische konsekwenties.
Met name is het nu mogelijk om bij het bedrijven van eindige elementen methoden
leentjebuur te spelen bij eindige volumen methoden.
Merk op dat we de specifieke vorm van de vektor $Q_x,Q_y$ redelijk open hebben
gelaten. Er is weliswaar gesuggereerd dat het hier om diffusie gaat, maar dit
gegeven is bij de afleiding ternauwernood gebruikt. Substitueer in plaats van
diffusie de konvektieve termen, en kijk hoe het tegenwind principe vertaald
moet worden in termen van eindige elementen. Dit programma is al gerealiseerd,
zelfs in 3-D [FTP].

