Allerlei logika

• Is there an established method for assigning a truth value $0 < t < 1$ to undecidable statements?

Zeker is dat althans de propositie-logika een zeer konkrete representatie heeft gevonden in de hardware van kombinatorische schakelingen. Zo komt de conjunctie van logische variabelen overeen met een serie-schakeling, de disjunctie met een parallel-schakeling (of omgekeerd). Samen met een complement-schakeling als "harde" ontkenning heeft men zo een kompleet stelsel van logische komponenten. Alle logische operaties kunnen worden uitgevoerd door serie- en parallel-schakelingen van deze komponenten te kombineren. Een dergelijke, als hardware gerealiseerde logika, is ruimtelijk van opbouw en brengt uitsluitend schakelingen voort welke statisch zijn in de tijd.

Louter met kombinatoriek kan men in de digitale techniek niet ver komen. Sequentiële schakelingen slaan de brug, van een logika in de ruimte, naar een logika in de tijd. Het geeft te denken dat juist op het punt van de sequentiële schakelingen de wegen van theorie en praktijk zich splitsen. Gezien vanuit de digitale techniek is de mathematische logika een volkomen statische theorie, welke als zodanig ongeschikt is om er de tijd-afhankelijkheid van flip-flops mee te beschrijven. In de schakeltechniek is men dan ook overgegaan tot de ontwikkeling van een geheel eigen wiskundig apparaat, dat met de gang van zaken in de mathematische logika verder geen enkel herkenbaar verband houdt [Flegg]. Vanuit deze invalshoek komt het voornaamste gebrek van de mathematische logika dus ogenblikkelijk aan het licht: gebrek aan dynamiek, in de tijd. Overigens is de logika in de tijd meer een kwestie van software dan van hardware.

De loop van een computer-programma wordt in belangrijke mate gestuurd door conditionele sprongopdrachten. Uitdrukkingen met "AND", "OR", en "NOT" komen voor, de logische kern echter wordt gevormd door statements van de gedaante "IF ... THEN ..." (: Basic, Cobol, Fortran). Nu is het bepaald geen geheim dat, bij formalisering van het redeneren volgens de mathematische logika [Tarski], diskrepanties ontstaan met het "als ... dan ..." van de omgangstaal. Verrassend is dat deze nadelige gevolgen van abstraktie zich niet voordoen bij het "IF ... THEN ..." van de hogere programmeertalen. Deze voorwaardelijke konstruktie sluit naadloos aan bij wat in de spreektaal ervan wordt verwacht. Is dit misschien de "formele" implikatie waar men in de mathematische logika voortdurend naar op zoek lijkt te wezen?

Stel dat dit zo is, dan is het bovendien mogelijk om ook de andere logische bewerkingen met behulp van 'formele' implicaties te definiëren. Dit gaat binnen de mathematische logika zelf met behulp van alleen de implicatie en de negatie. Bekend zijn namelijk de volgende formules: $$ P \vee Q \ \equiv \ \neg P \Rightarrow Q \qquad P \wedge Q \ \equiv \ \neg ( P \Rightarrow \neg Q) $$ Maar ook in een boek over het ontwikkelen van compilers [Gries] lezen wij, onder de vlag van het "optimaliseren van logische uitdrukkingen":

 c OR d   wordt gedefinieerd door  IF c THEN TRUE  ELSE  d
 c AND d  wordt gedefinieerd door  IF c THEN   d   ELSE FALSE
   NOT c  wordt gedefinieerd door  IF c THEN FALSE ELSE TRUE

 c ==> d  wordt gedefinieerd door  IF c THEN   d   ELSE TRUE
 c        wordt gedefinieerd door  IF c THEN TRUE  ELSE FALSE

De Boole algebra kan worden opgezet zonder in enigerlei opzicht te refereren aan het element-begrip.

Deze zienswijze wordt ondersteund alleen al door het feit dat de propositie-logika geheel kan worden geformuleerd in termen van dezelfde Boole algebra. Maar ook binnen de verzamelingenleer zelf heersen zekere gewoontes. Verzamelingstheoretische bewerkingen worden vaak geïllustreerd met behulp van zogenaamde Venn-diagrammen. Opvallend is dat bij deze visuele weergave er vrijwel altijd van wordt afgezien om ook de elementen te tekenen. Met andere woorden: bij stellingen die door genoemde "eierplaatjes" worden geïllustreerd - en dat zijn er nogal wat - abstraheert men als vanzelf van het elementbegrip. Stellingen van de Boole algebra worden op deze wijze, ook wanneer ze betrekking hebben op verzamelingen, elementloos gerepresenteerd. Zij weten dat niet, maar zij doen het [Marx].

We hebben hierboven gewezen op de grote tweespalt binnen de logische discipline: de theoretische mathematische logika aan de ene kant, de praktische logika van digitale schakelingen aan de andere kant. Typisch is nu dat in de schakeltechniek een unifikatie wordt bewerkstelligd tussen enerzijds zaken uit de mathematische logika (waarheidstafels) en anderzijds zaken uit de verzamelingenleer (Karnaugh diagram). Het precieze verband is wezenlijk eenvoudig. Logische variabelen $w, x, y, z$ worden tegelijkertijd opgevat als verzamelingen. Deze verzamelingen vormen met elkaar disjunkte doorsnijdingen, de zogenaamde "mintermen". Samen vullen deze mintermen het universum, als volgt voor twee variabelen (vier stuks): $$ ( \bar{x} \cap \bar{y} ) \cup ( \bar{x} \cap y ) \cup ( x \cap \bar{y} ) \cup ( x \cap y ) $$ Op grond van het voorgaande kunnen wij de mintermen echter voortaan betitelen ook als doodgewone elementen. Ze zijn immers niet leeg, ze zijn onderling disjunkt, en ze vullen een hele verzameling op.

Met de opvatting van een 4 x 4 Karnaugh diagram in het achterhoofd betekent een bitreeks als $(0101)$ één element van de zestien, namelijk het element $ (\bar{w} \cap x \cap \bar{y} \cap z) $. Anderzijds zijn er in alle moderne computers mogelijkheden aanwezig om op zulke bitreeksen Booleaanse bewerkingen toe te passen. Op het moment dat we dat doen, is $(0101)$ echter geen element meer, maar een verzameling. Stel dat we in totaal vier elementen $ w, x, y, z $ hebben, dan komt $(0101)$ overeen met $ \{ x , z \} $. We hebben hier iets heel merkwaardigs ontdekt:

Elementen en verzamelingen kunnen blijkbaar hun rollen omwisselen. Er is een dubbele opvatting mogelijk van de verhouding tussen element en verzameling. Het zijn eigenlijk duale begrippen.

Het is zeker geen toeval dat men in de wereld der gegevensbestanden (databases) al veel eerder op deze dualiteit gestuit is. Database Ontwerp [Bekke] is immers praktische verzamelingenleer bij uitstek, zou dat althans moeten zijn. Maar de verwarring in het vakgebied is groot. En de ontoepasselijke opzet van de klassieke verzamelingenleer is, ongetwijfeld, hoofdschuldige in dit drama. Het boek van ter Bekke geeft een goed overzicht, voor wie de kunst verstaat om tussen de regels door te lezen.

In boeken over schakeltechniek wordt vaak geen verschil gemaakt tussen verzamelingstheoretische operatoren aan de ene, en logische bewerkingen aan de andere kant. Wat zou er gebeuren als we deze werkwijze overnemen? Inderdaad kan op grond van de Boole algebra een één-één duidig verband worden gelegd tussen beide notatie-systemen. Wij maken een staatje op:

Verzamelingen	Leer	|	Mathematische	Logika
vereniging	$A \cup B$	|	of	$a \vee b$
doorsnede	$A \cap B$	|	en	$a \wedge b$
complement	$\bar{A}$	|	niet	$\neg a$
deelverzameling	$A \supset B$	|	impliceert	$a \Rightarrow b$
gelijkheid	$A=B$	|	equivalent	$a \Leftrightarrow b$

In de volgende figuur zien we de eierplaatjes van respektievelijk vereniging en doorsnede. Weinig schokkende beelden:

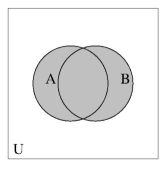
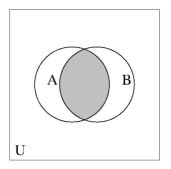
Ongewoner zijn de Venn diagrammen van deelverzameling en gelijkheid:

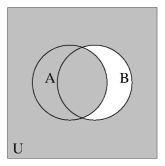
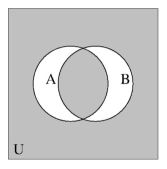
Het ongewone zit 'm in het feit dat nu ook $(A \supset B)$ en $(A = B)$ worden opgevat als bewerkingen in plaats van als relaties, precies zoals het geval is bij $ \cap $ en $ \cup $.
$(A \supset B)$ is een verzameling die bestaat uit de (Karnaugh-)elementen $ \{ \bar{A} \cap \bar{B} , A \cap \bar{B} , A \cap B \} $, met daarin niet $ \bar{A} \cap B $. Dit komt merkwaardigerwijs in het geheel niet overeen met de waarheidstabel voor de implicatie $ \Rightarrow $:

$ x \in A $	|	$ x \in B $	|	$ x \in (A \supset B ) $	|	$ (x \in A) \Rightarrow (x \in B) $
0	|	0	|	1	|	1
1	|	0	|	1	|	0
0	|	1	|	0	|	1
1	|	1	|	1	|	1

$(A = B)$ is een verzameling die bestaat uit de (Karnaugh-)elementen $ \{ \bar{A} \cap \bar{B} , A \cap B \} $, met daarin niet $ A \cap \bar{B} $ en $ \bar{A} \cap B $. Dit komt wel keurig overeen met de waarheidstabel voor de equivalentie $ \Leftrightarrow $:

$ x \in A $	|	$ x \in B $	|	$ x \in (A = B ) $	|	$ (x \in A) \Leftrightarrow (x \in B) $
0	|	0	|	1	|	1
1	|	0	|	0	|	0
0	|	1	|	|	0	0
1	|	1	|	1	|	1

Maar mischien is het onderstaande beeld toch meer in de lijn der verwachting, voor $(A \supset B )$ respectievelijk $(A = B$) :
 
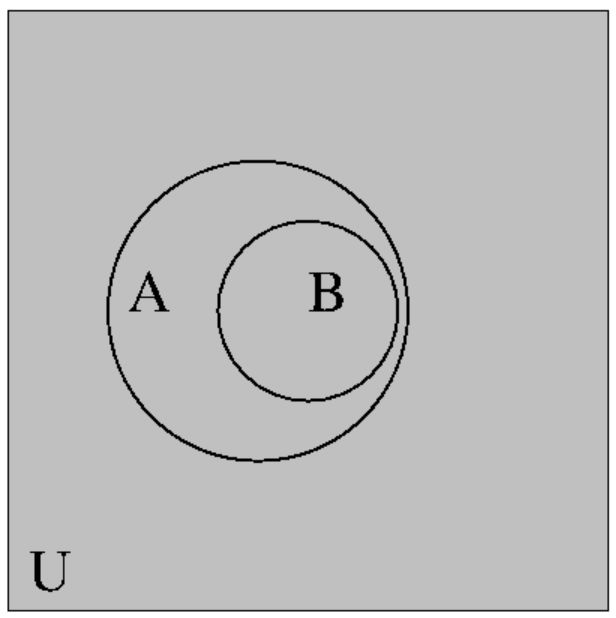
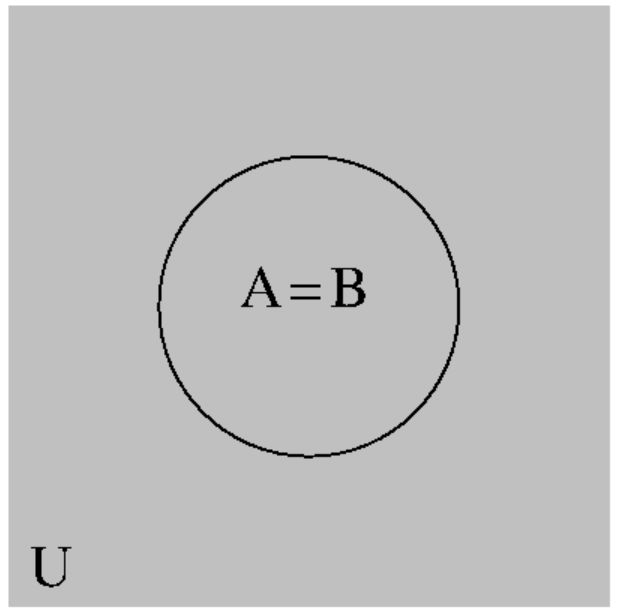
Er is wat voor te zeggen om $A \Rightarrow B$ op te vatten als de klassieke relatie $A \supset B$. "A impliceert B" betekent dan dat A ruimer is dan B en zodoende B omvat. Dit is mogelijk een andere weg om de "paradoxen der implicatie" [Tarski] te vermijden. Uit het bovenstaande blijkt reeds dat we in ieder geval met verschillende opvattingen (lees: waardetabellen) te maken hebben.
Voor de logische equivalentie geldt net zo, dat $A \Leftrightarrow B$ in alle redelijkheid zou kunnen worden opgevat als een gelijkheidsrelatie $A = B$.
Duaal aan deze opvatting van $=$ is de XOR bewerking, die in computer programma's, op machinetaal niveau wordt toegepast om te kijken of twee woorden $A$ en $B$ gelijk zijn. Is dit het geval, dan wordt $(A \: \mbox{XOR} \: B)$ gelijk aan 0, waarna meestal een voorwaardelijke sprong instruktie volgt.