Uniformity in polar coordinates

Processing math: 100%

Uniformity in polar coordinates

Imagine a polar web of similar quadrilaterals, as shown in the picture below:

Start with an innermost circle at a radial position

$R_0$ ; suppose that the mesh ends at a radial position

$R_N$ . Let the vertex points of the quadrilaterals in the mesh be given by:

$x_{i,j} = R_i\,\cos(\alpha_j) \quad ; \quad y_{i,j} = R_i\,\sin(\alpha_j)$ Where

$\alpha_j = j/M\cdot 2\pi$ with

$j = 0 , \cdots , M-1$ and

$i = 0 , \cdots , N$ . Then we have the following
Theorem. The radial positions in a mesh consisting of similar quadrilaterals are given by:

$R_i = R_0.\left(\frac{R_N}{R_0}\right)^{i/N} \qquad \mbox{where:} \quad i = 0, \cdots ,N$ Proof.

$R_0 = (R_N/R_0)^{0/N}$ and

$R_N = (R_N/R_0)^{N/N}$ to begin with.
In general, there are two edges of the quadrilaterals which have the same length, equal to:

$R_{i+1} - R_i = R_0.\left[ \left(\frac{R_N}{R_0}\right)^{(i+1)/N} - \left(\frac{R_N}{R_0}\right)^{i/N} \right] = R_i.\left[\left(\frac{R_N}{R_0}\right)^{1/N} - 1\right]$ Now

$\alpha_{j+1}-\alpha_j = 2\pi/M$ ; let

$c = (R_N/R_0)^{1/N}$ for short; then:

$R_{i+1} - R_i = R_i (c-1)$ .

The lengths of the two other edges of the quadrilaterals are (see above figure):

$R_i.2.\sin(\pi/M) \quad \mbox{and} \quad R_{i+1}.2.\sin(\pi/M) = R_i.c.2.\sin(\pi/M)$ Thus all edges scale up with only one variable factor

$R_i$ . Edges counterclockwise:

$R_i \times \left[\;2.\sin(\pi/M)\;,\;(c-1)\;,\;c.2.\sin(\pi/M)\;,\;(c-1)\;\right]$ Therefore all quadrilaterals have the same geometric shape. With other words: they are all similar. But we are not finished yet.

What we furthermore need is the following Lemma.
$w_a(x-A)^2+w_b(x-B)^2=(w_a+w_b)\left(x-\frac{w_aA+w_bB}{w_a+w_b}\right)^2+\frac{w_aw_b}{w_a+w_b}(A-B)^2$ Where $x,A,B$ and $w_a,w_b > 0$ are real numbers.
Proof. $w_a(x-A)^2+w_b(x-B)^2=\\ w_a(x^2-2Ax+A^2)+w_b(x^2-2Bx+B^2)=\\ (w_a+w_b)x^2-2(w_aA+w_bB)x+(w_aA^2+w_bB^2)=\\ (w_a+w_b)\left[x^2-2\frac{w_aA+w_bB}{w_a+w_b}+\left(\frac{w_aA+w_bB}{w_a+w_b}\right)^2\right] -(w_a+w_b)\left(\frac{w_aA+w_bB}{w_a+w_b}\right)^2+(w_aA^2+w_bB^2)=\\ (w_a+w_b)\left(x-\frac{w_aA+w_bB}{w_a+w_b}\right)^2 +\frac{-(w_aA+w_bB)^2+(w_a+w_b)(w_aA^2+w_bB^2)}{w_a+w_b}=\\ (w_a+w_b)\left(x-\frac{w_aA+w_bB}{w_a+w_b}\right)^2 +\frac{-(w_a^2A^2+2w_aw_bAB+w_b^2B^2)+w_a^2A^2+w_b^2B^2+w_aw_bA^2+w_aw_bB^2}{w_a+w_b}=\\ (w_a+w_b)\left(x-\frac{w_aA+w_bB}{w_a+w_b}\right)^2 +\frac{w_aw_b(A^2-2AB+B^2)}{w_a+w_b}=\\ (w_a+w_b)\left(x-\frac{w_aA+w_bB}{w_a+w_b}\right)^2+\frac{w_aw_b}{w_a+w_b}(A-B)^2$ Without Loss Of Generality (WLOG) we can put for the weighting factors: $w_1+w_2=1$ . 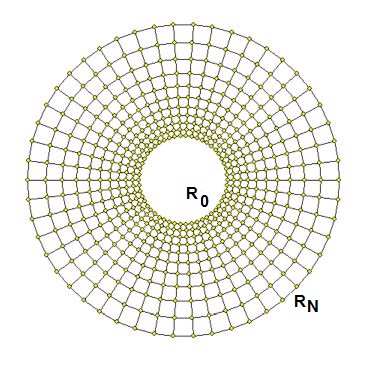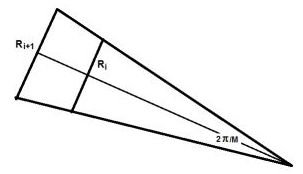Then we have: $w_a(x-A)^2+w_b(x-B)^2=\left[x-(w_aA+w_bB)\right]^2+w_aw_b(A-B)^2$ In particular when $\,w_1=w_2=1/2$ : $\frac{1}{2}\left[(x-A)^2+(x-B)^2\right]=\left(x-\frac{A+B}{2}\right)^2+\left(\frac{A-B}{2}\right)^2$ Application. We have found for the edges: $R_i \times \left[\;2.\sin(\pi/M)\;,\;(c-1)\;,\;c.2.\sin(\pi/M)\;,\;(c-1)\;\right]$ What we want now is to determine the constant $c$ in such a way that the following approximate equalities hold as good as possible: $2.\sin(\pi/M) \approx c-1 \quad \mbox{and} \quad c.2.\sin(\pi/M) \approx c-1$ Meaning that the quadrilaterals are similar to squares as good as possible. Formulated in a Least Squares sense, this in turn means that: $\frac{1}{2}\left[(x-A)^2+(x-B)^2\right] = \mbox{minimum}(c)$ with the substitutions $x = c-1$ , $A = 2.\sin(\pi/M)$ and $B = c.2.\sin(\pi/M)$ . The minimum is obviously attained when $x = (A+B)/2$ or: $c-1 = \sin(\pi/M)+c\sin(\pi/M) \quad \Longrightarrow \quad c\left[1-\sin(\pi/M)\right]=1+\sin(\pi/M) \quad \Longrightarrow \\ \frac{1+\sin(\pi/M)}{1-\sin(\pi/M)} = c = \left(\frac{R_N}{R_0}\right)^{1/N} \quad \Longrightarrow \quad \frac{R_N}{R_0} = \left(\frac{1+\sin(\pi/M)}{1-\sin(\pi/M)}\right)^N$ If the outer mesh radius is normed to one, ipse est $R_N=1$ , then we have for the inner mesh radius: $R_0 = \left(\frac{1-\sin(\pi/M)}{1+\sin(\pi/M)}\right)^N$