Fuzzyfied Polygons
$
\def \hieruit {\quad \Longrightarrow \quad}
\def \slechts {\quad \Longleftrightarrow \quad}
\def \half {\frac{1}{2}}
\def \MET {\qquad \mbox{where} \quad}
\def \VOOR {\qquad \mbox{for} \quad}
\def \EN {\quad \mbox{and} \quad}
$
Now let's try do the same for a circle with midpoint $(a,b)$ and radius $R$,
as approximated by an inscribed regular polygon with $N$ edges:
$$
C(x,y,\sigma) = \sum_{k=0}^{N-1} e^{-\half Q(x,y,t_k)/\sigma^2}\Delta t
\MET \Delta t = 2\pi/N \quad ; \quad t_k = k.\Delta t \\
\EN Q(x,y,t) = \left[x-a-R.\cos(t)\right]^2 + \left[y-b-R.\sin(t)\right]^2
$$
apart from a norming factor, which is often determined in practice as the maximum of $C(x,y,\sigma)$,
for fixed $\sigma$. But not necessarily so, as will be shown later.
It's advantageous to locate the midpoint of the circle at the origin and introduce dimensionless
coordinates:
$$
a = b = 0 \quad ; \quad (x,y) := \left(\frac{x}{R},\frac{y}{R}\right) \quad ; \quad \sigma := \frac{\sigma}{R}
$$
Resulting in:
$$
C(x,y,\sigma) = \sum_{k=0}^{N-1} e^{-\half \left\{\left[x-\cos(t_k)\right]^2 + \left[y-\sin(t_k)\right]^2\right\}/\sigma^2}\Delta t
\\ \MET \Delta t = 2\pi/N \quad ; \quad t_k = k.\Delta t
$$
There is no reason to introduce other variables than the ones currently in use, because
this is exactly the same as restricting the problem for a circle with unit radius.
When given the spread $\sigma$ of Gaussians and an inscribed $N$-gon,
the minimal value of $\sigma$ needed for blurring is known. For small angles $\Delta t$ it is
(with the first $\Delta$ as defined in the link):
$$
\sigma = \frac{\Delta}{2\pi}\alpha \hieruit \sigma \approx \alpha\frac{\Delta t}{2\pi}
\hieruit \sigma \approx \frac{\alpha}{N}
$$
Here $\alpha = \sqrt{2\:\ln(2\times 256)} \approx 3.5322$ is our standard blurring factor for Gaussians,
corresponding with the $256$ shades of gray
(:-) as present in true color graphics.
Larger angles are somewhat more complicated:
$$
\Delta = 2\sin(\Delta t/2) \hieruit \sigma = \frac{\sin(\pi/N)}{\pi}\alpha
$$
Hardly a (unit) circle anymore is the (unit) hexagon, but still then the first approximation is .. not so bad:
$$
\sigma = \frac{\sin(\pi/6)}{\pi}\alpha = \frac{\alpha}{2\pi} \approx \frac{\alpha}{6}
$$
We have also seen that only a neighborhood $\,\left|x-L.\Delta\right| < \alpha.\sigma\,$ (other notation!)
around $L.\Delta\,$ needs to be investigated, when evaluating terms of a Comb
of Gaussians. In terms of regular polygons:
$$
r = \sqrt{\left[x-\cos(t_k)\right]^2 + \left[y-\sin(t_k)\right]^2} < \alpha.\sigma
$$
This can be interpreted as $(x,y)$ inside a bunch of circles with midpoints $(\cos(t_k),\sin(t_k))$ and radius $\alpha.\sigma$.
It's easy to see that these circles are tangent to two other circles, namely:
$$
x^2+y^2 = (1-\alpha.\sigma)^2 \EN x^2+y^2 = (1+\alpha.\sigma)^2
$$
Which means that, given our tolerance $\epsilon$, it has only sense to calculate for:
$$
1-\alpha.\sigma < \sqrt{x^2+y^2} < 1+\alpha.\sigma
$$
With substantial savings in computing time as a result. Further time saving - but less than it may seem at first sight -
can be obtained by the following:
$$
r < \alpha.\sigma \approx \alpha\frac{\alpha}{N} \hieruit \frac{r}{2\pi/N} < \frac{\alpha^2}{2\pi} \approx 2
$$
This means that in the sum $\sum_{k=0}^{N-1}$ at most four ($=2\times 2$) angle increments are important,
provided that the increments are small, say less than those of a hexagon.
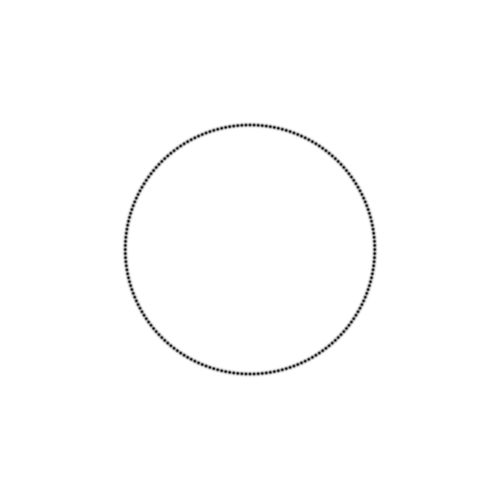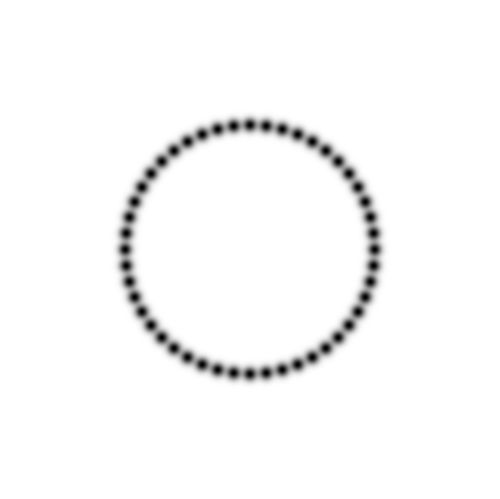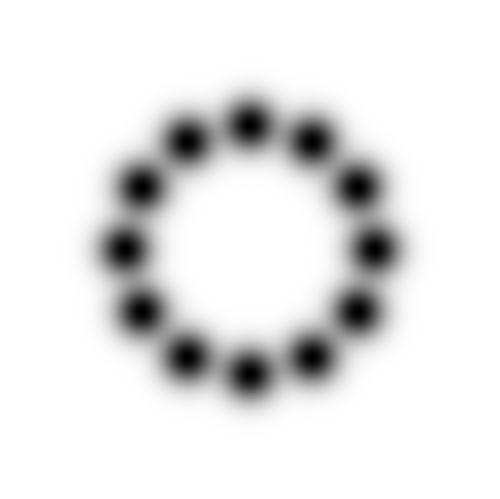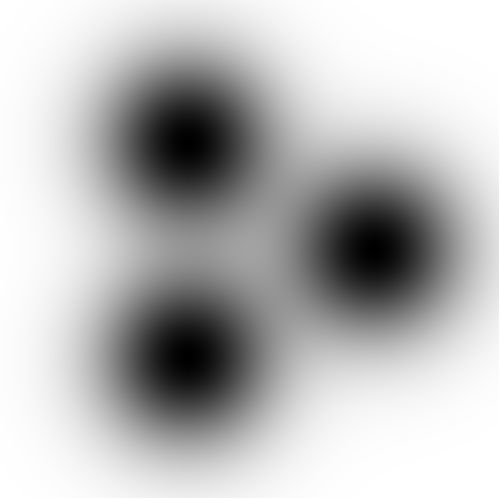
The rest - given our tolerance $\epsilon$ - is virtually invisible. There is software which does the slide show below.
It is started with a $3\times 512$ edged polygon. The number of edges is divided by two with each iteration, ending
with an equilateral triangle. The inscribed polygons are shown with each even iteration.
The viewport is defined by $-2 < x < +2$ and $-2 < y < +2$. It is seen that the fuzzyfication of regular polygons
can hardly be distinguised from the fuzzyfication of a circle. After all, this is precisely the gist of the present research.

The actual value of the spread $\sigma$ is critical. If only half of this value is taken, then continuity is lost,
as shall be apparent from the animation below.