Uniform Comb of Gaussians
$
\def \half {\frac{1}{2}}
\def \norm {\frac{1}{\sigma \sqrt{2\pi}} \; }
\def \MET {\qquad \mbox{where} \quad}
\def \hieruit {\quad \Longrightarrow \quad}
$
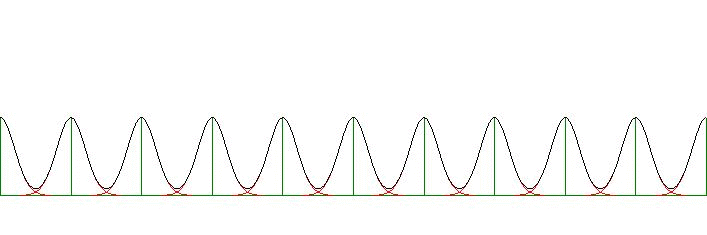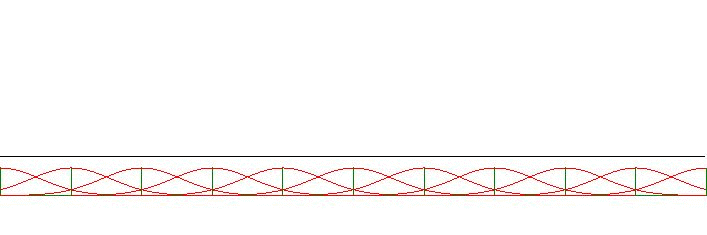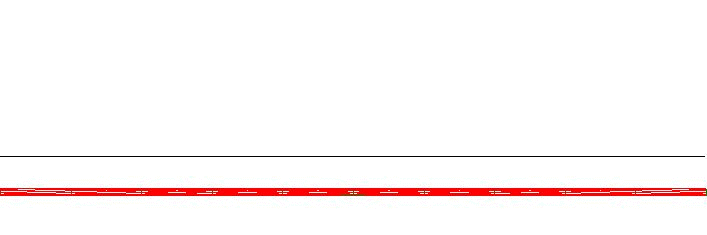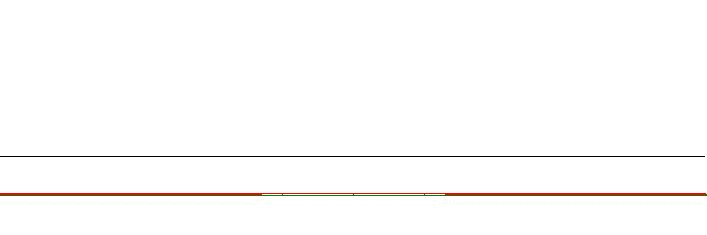
The subject of our current study are Combs of Bell shaped curves $P(x)$.
A very special but relevant case will be considered in the first place, namely
Gauss curves with a spread $\sigma$ , at a one-dimensional,
infinite and equidistant grid with discretization $\Delta$,
embedded in the real axis with coordinate $x$ :
$$
P(x) = \sum_{L=-\infty}^{+\infty} p(x-L.\Delta)\,\Delta
\MET p(x) = \norm e^{-\half\left(x/\sigma\right)^2}
$$
The function $P(x)$ can be interpreted as an attempt to "smooth" the uniform
density $x_L = L.\Delta$. Or "make fuzzy" the
discretization $f(x_L) = 1$ of a constant - and continuous - function $f(x) = 1$.
Check that $p(x)$ is normed. At first:
$$
\iint e^{-\half(x^2+y^2)/\sigma^2}dx\,dy =
\int_{-\infty}^{+\infty} e^{-\half x^2/\sigma^2}dx \int_{-\infty}^{+\infty} e^{-\half y^2/\sigma^2}dy =
\left[\int_{-\infty}^{+\infty} e^{-\half x^2/\sigma^2}dx\right]^2
$$
On the other hand, introducing polar coordinates:
$$
\iint e^{-\half(x^2+y^2)/\sigma^2}dx\,dy = \iint e^{-\half r^2/\sigma^2}r\,dr\,d\phi =
\int_0^\infty e^{-\half(r/\sigma)^2} d\left[\half(r/\sigma)^2\right]\,\sigma^2\int_0^{2\pi}d\phi = 2\pi\sigma^2
$$
Hence:
$$
\left[\int_{-\infty}^{+\infty} e^{-\half x^2/\sigma^2}dx\right]^2 = 2\pi\sigma^2 \hieruit
\norm \int_{-\infty}^{+\infty} e^{-\half x^2/\sigma^2}dx = 1
$$
Check that the standard deviation / spread is $\,\sigma\,$:
$$
\overline{x^2} = \norm \int_{-\infty}^{+\infty} e^{-\half x^2/\sigma^2} x^2 dx =
-\sigma^2\,\norm \int_{-\infty}^{+\infty} e^{-\half x^2/\sigma^2}\,x\,d\left[-\half (x/\sigma)^2\right] = \\
-\sigma^2\,\norm \int_{-\infty}^{+\infty} x\,d\left(e^{-\half x^2/\sigma^2}\right) =
\norm \left[x\,e^{-\half x^2/\sigma^2}\right]_{-\infty}^{+\infty}
+ \sigma^2\,\norm \int_{-\infty}^{+\infty} e^{-\half x^2/\sigma^2} \,dx \\ \hieruit \overline{x^2} = \sigma^2
$$
The Fourier series for a comb of Gaussian distributions is:
$$
P(x) = 1 + 2 \times \sum_{k = 1}^{\infty} A(k \omega) \, cos(k \omega x)
$$
Where it is reminded that $\omega = 2\pi / \Delta$. And:
$$
A(y) = \int_{- \infty}^{+ \infty} p(x) \cos(y x) \, dx
= \norm \int_{-\infty}^{+\infty} e^{-\half x^2/\sigma^2} \cos(y x) \, dx
$$
The latter integral equals to:
$$
A(y) = \norm \int_{-\infty}^{+\infty} e^{-\half x^2/\sigma^2} e^{i y x} \, dx =
\norm \int_{-\infty}^{+\infty} e^{ -\half x^2/\sigma^2 + i y x } \, dx
$$
The argument in the exponent is treated separately:
$$
-\half x^2/\sigma^2 + i y x = -\half \left[(x/\sigma)^2 - 2(\sigma.iy)(x/\sigma) + (\sigma.iy)^2\right] +\half (\sigma.iy)^2
= -\half (x-\sigma^2.iy)^2/\sigma^2 - \half \sigma^2 y^2
$$
It follows that:
$$
A(y) = e^{-\half \sigma^2 y^2} \norm \int_{-\infty}^{+\infty} e^{-\half (x-\mu)^2/\sigma^2} dx
\quad \mbox{with} \quad \mu = \sigma^2.iy \hieruit A(y) = e^{-\half \sigma^2 y^2}
$$
Where it is tacitly assumed that a complex shift $\,\mu\,$ is like a real valued shift $\,\mu\,$
i.e. it does not change the outcome of the normed integral $=1$.
Conclusion, for a Uniform Comb of Gaussians $\,p\,$, with discretization $\,\Delta\,$ and $\,\omega = 2\pi / \Delta\,$:
$$
P(x) = \sum_{L = -\infty}^{+\infty} p(x - L \Delta)\,\Delta =
1 + 2 \times \sum_{k = 1}^{\infty} e^{-\half (k\omega\sigma)^2} \cos(k\omega x)
$$
As has been said, the Uniform Comb of Gaussians can - or rather maybe should -
be interpreted as an attempt to "make continuous again" the discrete function
$p(x_L = L.\Delta) = 1$ . The latter may be considered as the discretization or
sampling of a continuous (constant) function : $\,p(x) = 1\,$. Thinking along
these lines, a natural question is "how good" the continuization achieved
by the Comb of Gaussians will be, depending on the sampling frequency $\,\omega =
2\pi/\Delta\,$ and the spread $\,\sigma\,$. It is expected that the Fourier Analysis
of the preceding section will give us kind of a clue about it:
$$
P(x) = \frac{\Delta}{\sigma\sqrt{2\pi}}
\sum_{L = -\infty}^{+\infty} e^{-\half(x-L\Delta)^2/\sigma^2} =
1 + 2 \times \sum_{k=1}^{\infty}
e^{-\half(k\omega\sigma )^2}\,\cos(k\omega x)
$$
It is seen that $P(x)$ is approximately equal to one, indeed,
provided that the next term is sufficiently
small. First we take, out of thin air, an "acceptable" (relative) error,
called $\,\epsilon (> 0)\,$. As the next step, we require that the (amplitude of)
the second term (for $\,k=1\,$) is smaller than the error:
$$
2 \times e^{-\half(\omega\sigma )^2} < \epsilon
\hieruit - \half (\omega\sigma)^2 < \ln(\epsilon/2)
$$ $$
\hieruit (\frac{2\pi}{\Delta}\sigma)^2 > 2\:\ln(2/\epsilon)
\hieruit \sigma > \frac{\Delta}{2\pi}\sqrt{2\:\ln(2/\epsilon)}
$$
The quantity $\,\alpha\,$ (alpha) is defined as:
$$
\alpha = \sqrt{2\:\ln(2/\epsilon)}
\hieruit \sigma > \frac{\Delta}{2\pi}\alpha
$$
Luckily for everybody, $\,\alpha\,$ is varying very slowly as a function of
$\,\epsilon\,$. Therefore it's not necessary to determine that error very
precise, in order to have quite a good estimate of the spread $\sigma$ in the
Gaussians. The typical thing is, though, that we really need a finite
error. For if $\epsilon$ could be zero, then $\alpha$ would become infinite
and the whole theory would evaporate into nothingness. Therefore it's impossible
to make the discrete continuous in a mathematics without errors.
Out of thin air .. When visualizing the results of such a "fuzzyfication" as
a gray valued image, the Comb is always "normed", meaning that all values are
divided by their maximum value. Thus maximum values are made equal to $ = 1$,
corresponding with black pixels. A natural error with such gray valued images
is the lowest increment in grayness, which on a scale ranging from $0$ to $1$
is equal to $1/256$ . Hence, in this case: $\alpha = \sqrt{2\:\ln(512)} \approx
3.53223$ , a value which is used throughout in the software accompanying this
article.
Another issue is computational efficiency with summing the terms of the Comb.
So let's investigate where the values of a Gaussian can be neglected, when
compared with our acceptable error (divided by $2$ for even better accuracy -
we employ the fact that $\alpha$ is rather insensitive to precise values and
we prefer to define it once and forever):
$$
e^{-\half\left[(x-L.\Delta)/\sigma\right]^2} < \epsilon/2 \hieruit
\left[(x-L.\Delta)/\sigma\right]^2 > 2\,\ln(2/\epsilon) \hieruit
$$ $$
\left| x - L.\Delta \right| > \sigma \sqrt{2\:\ln(2/\epsilon)} = \alpha.\sigma
$$
This means that only a neighborhood $\,\left|x-L.\Delta\right| < \alpha.\sigma\,$
around $L.\Delta\,$ needs to be investigated, when evaluating terms of the Comb
of Gaussians.
