Calculation reveals that the absolute maximum $(\sigma,C(0,\sigma)$ on the left is obtained for:
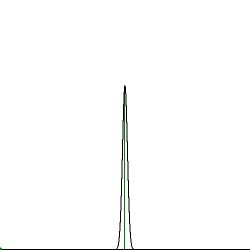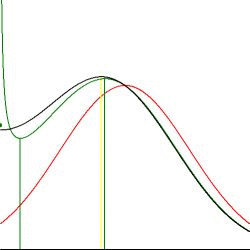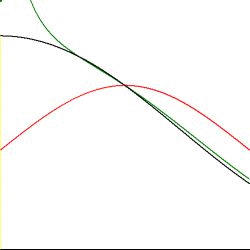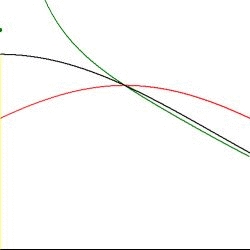
Spread = 0.928748860045918 Center = 1.30771428741129Other data obtained are the values $(\sigma,C(0,\sigma))$ at the center and the values $(r_m,C(r_m,\sigma))$ of the relative maxima, as indicated with the vertical yellow lines. The meaning of the red and green lines shall be explained below. All relative maxima are inside the (unit) circle, moving towards the center, and they are increasing until $\sigma = 0.928748860045918$ and then decreasing, at the center, with increasing $\sigma$, finally converging slowly to one $=1$ overall: $$ \lim_{\sigma\to\infty} C(r,\sigma) = \lim_{\sigma\to\infty} e^{-\half(r-1)^2/\sigma^2} \frac{\sum_{k=0}^{N-1} \lim_{\sigma\to\infty} e^{r\left[\cos(k.2\pi/N)-1\right]/\sigma^2}} {\sum_{k=0}^{N-1} \lim_{\sigma\to\infty} e^{\left[\cos(k.2\pi/N)-1\right]/\sigma^2}} = e^0\frac{Ne^0}{Ne^0}=1 $$ There is always a local minimum or maximum at the center with horizontal tangent, because apart from the norming factor we have: $$ \left.\frac{\partial C}{\partial r}\right|_{r=0} = -\frac{r-1}{\sigma^2}e^{-\half(r-1)^2/\sigma^2} \sum_{k=0}^{N-1}e^{r\left[\cos(k.2\pi/N)-1\right]/\sigma^2} + e^{-\half(r-1)^2/\sigma^2} \sum_{k=0}^{N-1}\frac{\cos(k.2\pi/N)-1}{\sigma^2} e^{r\left[\cos(k.2\pi/N)-1\right]/\sigma^2} \\ = \frac{1}{\sigma^2}e^{-1/(2\sigma^2)}.N + \frac{1}{\sigma^2} e^{-1/(2\sigma^2)} \left[\sum_{k=0}^{N-1} \cos(k.2\pi/N) - N\right] = 0 $$ It is somewhat unsatisfactory that a large sum has to be calculated for the purpose of defining a norming factor. After all, that sum is by far not so large as it seems. We have seen in Fuzzyfied Polygons, (with another definition for $r$) that: $$ r < \alpha.\sigma \approx \alpha\frac{\alpha}{N} \hieruit \frac{r}{2\pi/N} < \frac{\alpha^2}{2\pi} \approx 2 $$ This means that in the sum $\sum_{k=0}^{N-1}$ only a few, say four, angle increments are important. Let us now approximate the sum of the norming factor by an integral: $$ C(1,\sigma) = \frac{2\pi}{N} \sum_{k=0}^{N-1}e^{\left[\cos(k.2\pi/N)-1\right]/\sigma^2} \approx \int_0^{2\pi} e^{\left[\cos(t)-1\right]/\sigma^2} dt = \int_{-\pi}^{+\pi} e^{\left[\cos(t)-1\right]/\sigma^2} dt $$ The finding that only a few increments around $t=0$ play a role may be translated in two things. At first we have that only a few terms of the series development for $\cos(t)$ are significant. Second we have that around $t=0$ positive angles quickly appear to be large, that is infinity, and negative angles (or angles somewhat below $2\pi$) quickly appear to be minus infinity, ipse est $\pi \approx \infty$ in the rightmost integral. Both arguments indeed give rise to a much simplified expression for the norming factor, if we want to replace it eventually: $$ \cos(t) \approx 1-\half t^2 \hieruit C(1,\sigma) \approx \int_{-\infty}^{+\infty} e^{-\half t^2/\sigma^2} dt = \sigma\sqrt{2\pi} $$ In very much the same way an analytical expression for the other integral candidate can be found as well: $$ \frac{2\pi}{N} \sum_{k=0}^{N-1} e^{r\left[\cos(k.2\pi/N)-1\right]/\sigma^2} \approx \int_0^{2\pi} e^{r\left[\cos(t)-1\right]/\sigma^2} dt \approx \int_{-\infty}^{+\infty} e^{-\half t^2/(\sigma/\sqrt{r})^2} dt = \frac{\sigma\sqrt{2\pi}}{\sqrt{r}} $$ Resulting in the following simple estimate for the normed solution (mind the color in the animation): $$ \color{green}{C(r,\sigma) \approx e^{-\half(r-1)^2/\sigma^2}/\sqrt{r}} $$ It should be expected that this estimate is bad for $r=0$, the midpoint of the circle, but there we have an exact outcome for the sum - depicted as a little green spot: $$ \frac{2\pi}{N} \sum_{k=0}^{N-1} e^{0\left[\cos(k.2\pi/N)-1\right]/\sigma^2} = 2\pi \hieruit C(0,\sigma) \approx \frac{\sqrt{2\pi}}{\sigma} e^{-1/(2\sigma^2)} $$ We repeat. Calculation has revealed that the absolute maximum $(\sigma,C(0,\sigma)$ is obtained for:
Spread = 0.928748860045918 Center = 1.30771428741129With our analytical approximation we have: $$ \frac{d C(0,\sigma)}{d\sigma} \approx \frac{d}{d\sigma}\left[\frac{\sqrt{2\pi}}{\sigma} e^{-1/(2\sigma^2)}\right] = -\frac{\sqrt{2\pi}}{\sigma^2} e^{-1/(2\sigma^2)} + \frac{\sqrt{2\pi}}{\sigma}\left[+\half.2.\sigma^{-3}\right] e^{-1/(2\sigma^2)} = 0 \\ \times e^{+1/(2\sigma^2)}/\sqrt{2\pi}.\sigma^4 \hieruit -\sigma^2+1 = 0 \hieruit \sigma = 1 $$ Which is indeed reasonably close to the "exact" value: $0.928748860045918$. Now calculate for the maximum and judge for yourself how good it is: $$ C(0,1) \approx e^{-1/2}\sqrt{2\pi} = \sqrt{2\pi/e} \approx 1.520346901 $$ Employing the other approximation we might try to calculate analogously the values $(r_m,C(r_m,\sigma))$ of the relative maxima, as indicated with the vertical yellow lines in the above animation. But there is more. $$ \frac{d C(r,\sigma)}{dr} \approx \frac{d}{dr} \left[e^{-\half(r-1)^2/\sigma^2}/\sqrt{r}\right] = -\frac{r-1}{\sigma^2\sqrt{r}} e^{-\half(r-1)^2/\sigma^2} - e^{-\half(r-1)^2/\sigma^2} \frac{1}{r\sqrt{r}} \\ \times \left[-e^{+\half(r-1)^2/\sigma^2} \sigma^2 r\sqrt{r}\right] \hieruit (r-1)r+\half\sigma^2 = 0 \hieruit r = \half\pm\half\sqrt{1-2\sigma^2} $$ With the root $r=1/2+1/2\sqrt{1-2\sigma^2}$, for $\sigma\to 0$ we have the unit circle. It is seen that, for the relative maxima, there is indeed a shift to the left for increasing values of $\sigma$, as shown in the animation. With the analytical approximation, though, there is a maximum value for $\sigma$, namely $\sigma = 1/\sqrt{2}$, corresponding with a minimal value $1/2$ for $r$ as well. Not so in the more precise numerical solution.
> r := 1/2+1/2*sqrt(1-2*sigma^2); > C(sigma) := exp(-(r-1)^1/sigma^2/2)/sqrt(r); > D(sigma) := simplify(diff(C(sigma),sigma));Resulting in the following expression: $$ \frac{dC(r_m,\sigma)}{d\sigma} = \frac{e^{-1/4\,(-1+\sqrt{1-2\,\sigma^2})/\sigma^2}\left(1-\sqrt{1-2\,\sigma^2}+2\,\sigma^2\right)} {\sigma\,\sqrt{1-2\,\sigma^2}\left(1+\sqrt{1-2\,\sigma^2}\right)\sqrt{2+2\,\sqrt{1-2\,\sigma^2}}} $$ Continuing by hand, it becomes clear that the whole thing is indeed positive: $$ = \frac{e^{-1/4\,(-1+\sqrt{1-2\,\sigma^2})/\sigma^2}\left(1-\sqrt{1-2\,\sigma^2}\right)\left(2+\sqrt{1-2\,\sigma^2}\right)} {\sigma\,\sqrt{1-2\,\sigma^2}\left(1+\sqrt{1-2\,\sigma^2}\right)\sqrt{2+2\,\sqrt{1-2\,\sigma^2}}} > 0 $$ Therefore the relative maxima are increasing with increasing spread $0 < \sigma < 1/\sqrt{2}$.