Explanation - everything real-valued:
$$
(x,y) = \mbox{cartesian coordinates} \\
\phi = \mbox{angle, in polar coordinates} \\
H(x) = \begin{cases} 0 & \mbox{for} & x < 0 \\ 1 & \mbox{for} & x > 0 \end{cases} \quad \mbox{: Heaviside function}\\
\delta(y) = \begin{cases} 0 & \mbox{for} & y \ne 0 \\ \infty & \mbox{for} & y = 0 \end{cases} \quad \mbox{and} \quad
\int_{-\infty}^{+\infty} \delta(y) \,dy = 1 \quad \mbox{: Dirac delta}
$$
The meaning of the formula is a topological one:
Crossing number = Winding number
Here is a visualization. WLOG the origin $(0,0)$ is taken at the black dots inside/outside a domain.
The integrations are carried out over the boundary of that domain.
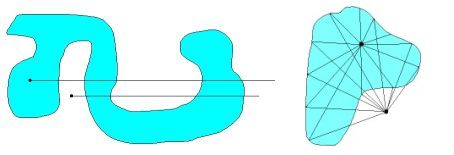
A proof of the formula is found
at this place.
I want to know if this formula has been found by others (< 2005); any references would be quite welcome.

