What the OP really wants, I think, is a crossing number algorithm for a simple closed continuous curve.
Such a curve can be considered, however, as the limiting case of a simple polygon, for its edges becoming
infinitesimally small. A relevant reference therefore may be this Wikipedia one:
and especially the crossing number algorithm.
But there is much more to tell about the Inside / Outside Problem, once you take a good look at it.
After some (in vain) attempts to answer the question in a concise manner, and while making too many duplicates
of existing material, I've decided to simply redirect to my best shot so far:
If the points of the simple closed curve are considered as pixels (i.e. integer coordinates),
then we can even devise a never fail algorithm (only assuming that our picture is not too large).
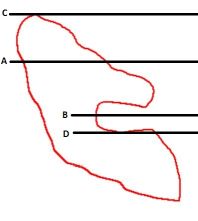
It is seen in the picture below that, for a continuous curve, simple and straightforward application
of the crossing number algorithm will be OK for the points $A$ and $B$, but it certainly will go wrong for the points $C$ and $D$.
According to Murphy's law ,
Anything that can go wrong will go wrong. Meaning that ignoring special cases,
especially in a computational geometry environment, sooner or later, will be disastrous.
It is noticed that the "wrong" cases have to do with rays that are tangent to the curve.