Apart from the observation that the two methods seem to be (or rather should be) equivalent,
using the Delaunay triangulation, without the Voronoi detour, seems to be the most straightforward.
Furthermore it is more convenient to first determine the integral over
one (Delaunay) triangle and then simply sum up over all triangles;
nothing is gained with gathering triangles at the same vertex, for the reason that a summation of numbers can be in any order.
Precise formulation for one triangle $\Delta$ with vertices $(x_1,y_1),(x_2,y_2),(x_3,y_3)$
and function values $(f_1,f_2,f_3)$ at these vertices (in case you didn't know this already):
$$
\iint_{\Delta} f(x,y)\,dx\,dy = \frac{1}{2}
\det\begin{bmatrix} (x_2-x_1) & (x_3-x_1) \\ (y_2-y_1) & (y_3-y_1) \end{bmatrix}
\frac{f_1+f_2+f_3}{3}
$$
Then sum up over all triangles in the domain / mesh $\Omega$ :
$$
\iint_{\Omega} f(x,y)\,dx\,dy = \sum_{\Delta} \iint_{\Delta} f(x,y)\,dx\,dy
$$
And that's it. So I'd vote for your approach, apart from minor details.
Sideways note. Actually, Delaunay triangles and Voronoi regions are
dual to each other.
The former concept is the more favorite with Finite Element Methods,
while the latter concept is the more favorite with Finite Difference/Volume methods. My personal bias is the unification of both;
Voronoi regions are at page 13 in the following reference :
2-D Elementary Substructures .
Delaunay and Voronoi regions.
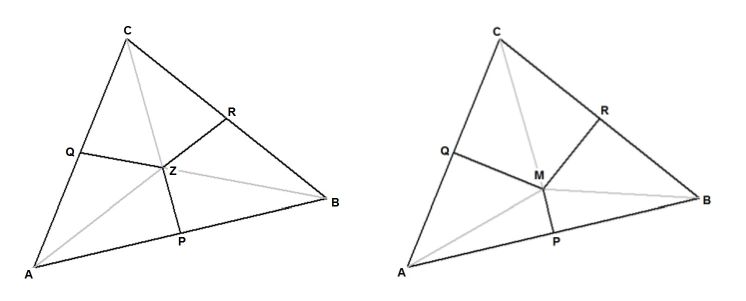
- Picture on the left: (Delaunay) triangle with medians
and regions tentatively called Delaunay regions
(hoping this nomenclature has not been claimed already somewhere)
- Picture on the right: same triangle with perpendicular
bisectors and Voronoi regions
It is easy to show that the area of a Delaunay region is $1/3 \times$
the area of the (Delaunay) triangle.
Proof. Without loss of generality,
let $A = (0,0)$ , $B = (x_B,y_B)$ , $C = (x_C,y_C)$ , then the
area of e.g. the Delaunay region $APZQ$ is:
$$
\frac{1}{2} \det\begin{bmatrix} x_B/2 & (x_B+x_C)/3 \\ y_B/2 & (y_B+y_C)/3 \end{bmatrix} +
\frac{1}{2} \det\begin{bmatrix} (x_B+x_C)/3 & x_C/2 \\ (y_B+y_C)/3 & y_C/2 \end{bmatrix} =
\frac{1}{3} \times \frac{1}{2} \det\begin{bmatrix} x_B & x_C \\ y_B & y_C \end{bmatrix}
$$
So we may safely conclude that the numerical integration procedure
as proposed in this answer is equivalent with numerical integration
over Delaunay regions (collected around a vertex).
Finding the area of a Voronoi region is far more complicated (I think).
It is clear from the pictures, however, that weighting function
values with Delaunay regions is at least different from
weighting function values with Voronoi regions (except for equilateral triangles).
UPDATE. Without loss of generality again, let $A = (0,0)$ , $B = (x_B,y_B)$ , $C = (x_C,y_C)$ , then the
area of e.g. the Voronoi region $APMQ$ is:
$$
V = \frac{\left[(x_B^2+y_B^2) - (x_B x_C + y_B y_C)\right]\left[x_C^2+y_C^2\right]}
{8(x_B y_C- y_B x_C)} +
\frac{\left[(x_C^2+y_C^2) - (x_B x_C + y_B y_C)\right]\left[x_B^2+y_B^2\right]}
{8(x_B y_C- y_B x_C)}
$$
Coded in a little (Delphi) Pascal program - the function call $V(A,B,C)$ is to be memorized:
program Voronoi;
type
point = record
x,y : double;
end;
function V(A,B,C : point) : double;
{
Area of Voronoi Region
in Delaunay triangle
}
var
O1,O2 : double;
p,q : point;
begin
p.x := B.x-A.x; p.y := B.y-A.y;
q.x := C.x-A.x; q.y := C.y-A.y;
O1 := (-q.y*p.y+p.x*p.x+p.y*p.y-p.x*q.x)*(q.x*q.x+q.y*q.y)
/ (p.x*q.y-p.y*q.x)/8;
O2 := (-q.y*p.y+q.x*q.x+q.y*q.y-p.x*q.x)*(p.x*p.x+p.y*p.y)
/ (p.x*q.y-p.y*q.x)/8;
V := O1+O2;
end;
procedure test;
{
Sum of Voronoi areas must be
Area of Delaunay triangle
}
var
A,B,C,p,q : point;
begin
Random; Random;
p.x := Random; p.y := Random;
q.x := Random; q.y := Random;
A.x := 0; A.y := 0;
B.x := p.x; B.y := p.y;
C.x := q.x; C.y := q.y;
Writeln(V(A,B,C) + V(B,C,A) + V(C,A,B),
' =',(p.x*q.y-p.y*q.x)/2);
end;
begin
test;
end.
Thus, quite in general, the numerical integration procedure is as follows:
$$
\iint_{\Delta} f(x,y)\,dx\,dy = w_1 f_1 + w_2 f_2 + w_3 f_3 \qquad ; \qquad
\iint_{\Omega} f(x,y)\,dx\,dy = \sum_{\Delta} \iint_{\Delta} f(x,y)\,dx\,dy
$$
Where:
- $w_1=w_2=w_3=1/3 \times$ area of triangle , for the Delaunay regions approach
- $w_1 = V(A,B,C)\, , w_2 = V(B,C,A)\, , w_3 = V(C,A,B)$ , for the Voronoi regions approach
Consider all Delaunay / Voronoi regions around a vertex. For simplicity, assume that
the associated triangles form a regular polygon with $N$ edges,
such that each top angle of a triangle is $\phi=2\pi/N$ . All
triangles are isoceles, hence $\;x_B^2+y_B^2=x_C^2+y_C^2=L^2\;$ and we can
easily determine the ratio ( area of a Delaunay region ) / ( area of Voronoi region ) ,
with the cosine rule for an inner product and the sine rule for a determinant:
$$
\frac{L^2\sin(\phi)/2/3}{2\left[L^2-L^2\cos(\phi)\right]L^2/\left[8L^2\sin(\phi)\right]} =
\frac{2}{3}\frac{\sin^2(\phi)}{1-\cos(\phi)} \quad \Longrightarrow \\
\frac{\mbox{Delaunay}}{\mbox{Voronoi}} = \frac{2}{3}\left[\,1+\cos(\phi)\,\right]
$$
It follows that Delaunay = Voronoi for $\,1+\cos(\phi) = 3/2\,$ hence $\,\phi=\pi/3$ ,
as expected (equilateral triangles) . Furthermore Delaunay > Voronoi for $\,\phi<\pi/3\,$
and Voronoi > Delaunay for $\,\phi>\pi/3$ . Especially for obtuse triangles (negative cosine) the ratio
can become nearly zero, which means that the Voronoi regions can become much
larger than the Delaunay regions, thereby giving a seemingly unreasonable high weight
to an associated function value.
Let $\;a=\sqrt{x_B^2+y_B^2}\;$ and $\;b=\sqrt{x_C^2+y_C^2}\;$ . Then for those who want the above WLOG :
$$
\frac{\mbox{Delaunay}}{\mbox{Voronoi}} =
\frac{4/3\,a^2b^2\left[1-\cos^2(\phi)\right]}{2a^2b^2-ab(a^2+b^2)\cos(\phi)}
$$
Solving for the three cases $\;<1,=1,>1\;$ is then equivalent with solving a quadratic equation
for $<0,=0,>0$ , i.e. where the following parabola is positive/zero/negative, with $\;x=\cos(\phi)$ :
$$
y = x^2-\frac{3}{4}\frac{a^2+b^2}{ab}x+\frac{1}{2}
$$

