How fat is a triangle?

After all those appetizer comments of mine, the OP himself is asking for : what formula describes the slimness of a triangle, based on Steiner Ellipses? So it's time to feed some meat to the public :-)
Needed for the Steiner ellipse, or best fit ellipse, or ellipse of inertia (they are all similar) are the variances (in statistics terms) of moments of inertia (in physics terms). To calculate the latter, there are three possibilities:
  1. Simplest case: all triangle weight is in the vertices $(x_1,y_1),(x_2,y_2),(x_3,y_3)$
  2. The triangle consists of three rods and all weight is in there
  3. The triangle is cut from a plate and the weight is distibuted uniformly over its area
The area point of view has been worked out in the reference Steiner Ellipses and Variances. At the last page of this reference is also the important statement that the best fit ellipse of a triangle is an inertial ellipse and is the inner Steiner ellipse. For simplicity, we shall adopt the weight at vertices case here. See the reference, or work out the second case yourself, if you want otherwise. $$ \mu_x = (x_1+x_2+x_3)/3 \quad ; \quad \mu_y = (y_1+y_2+y_3)/3 \\ \sigma_{xx} = (x_1^2+x_2^2+x_3^2)/3 - \mu_x^2 = \frac{2}{9}(x_1^2+x_2^2+x_3^2-x_1x_2-x_1x_3-x_2x_3) \\ \sigma_{yy} = (y_1^2+y_2^2+y_3^2)/3 - \mu_y^2 = \frac{2}{9}(y_1^2+y_2^2+y_3^2-y_1y_2-y_1y_3-y_2y_3) \\ \sigma_{xy} = \left[(x_1-\mu_x)(y_1-\mu_y)+(x_2-\mu_x)(y_2-\mu_y)+(x_3-\mu_x)(y_3-\mu_y)\right]/3 = \\ \frac{1}{9}(2x_1 y_1 + 2x_2 y_2 + 2x_3 y_3 - x_1 y_2 - x_2 y_1 - x_2 y_3 - x_3 y_2 - x_1 y_3 - x_3 y_1) $$ The best fit ellipse of inertia is: $$ \frac{\sigma_{yy}(x-\mu_x)^2 - 2\sigma_{xy}(x-\mu_x)(y-\mu_y) + \sigma_{xx}(y-\mu_y)^2} {\sigma_{xx}\sigma_{yy}-\sigma_{xy}^2} = 2 $$ The eigenvalues of the covariance matrix (of inertia) are related to the axes of the ellipse: $$ \left| \begin{matrix} \sigma_{xx}-\lambda & \sigma_{xy} \\ \sigma_{xy} & \sigma_{yy}-\lambda \end{matrix} \right| = 0 \qquad \Longleftrightarrow \qquad \lambda^2 - (\sigma_{xx}+\sigma_{yy})\lambda + (\sigma_{xx}\sigma_{yy}-\sigma_{xy}^2) = 0 $$ Rename (Trace and Determinant): $$ \mbox{Tr} = \sigma_{xx}+\sigma_{yy} \qquad ; \qquad \mbox{Det} = \sigma_{xx}\sigma_{yy}-\sigma_{xy}^2 $$ Then the solutions are (very much real and positive): $$ \lambda_{\pm} = \mbox{Tr}/2 \pm \sqrt{\left(\mbox{Tr}/2\right)^2 - \mbox{Det}} $$ The excentricity of the ellipse is: $$ \epsilon = \sqrt{\frac{\lambda_{+}}{\lambda_{-}}} = \frac{\sqrt{\lambda_{+}\lambda_{-}}}{\lambda_{-}} = \frac{\sqrt{\mbox{Det}}}{\lambda_{-}} = \frac{\lambda_{+}}{\sqrt{\mbox{Det}}} $$ Which is the formula you asked for (hopefully).
(Un)fortunately I have only a program that generates pictures for the case that the weight of the triangle is uniformly distributed over its area (which anyway seems to be the more interesting):

Update. It may be questioned if choosing one of the triangle views, as 3 vertices (1), as 3 rods (2), as a flat plate (3), has any influence on the slimness factor.
It can be easily proved that the center of gravity / midpoint of the triangle in all three cases is the same : $\mu_x = (x_1+x_2+x_3)/3 \; ; \; \mu_y = (y_1+y_2+y_3)/3$ . Now define the following quantities, where it is noted that the last two can be derived from the first one: $$ s_{xy} = (x_1-x_2)(y_1-y_2)+(x_2-x_3)(y_2-y_3)+(x_3-x_1)(y_3-y_1) \\ s_{xx} = (x_1-x_2)^2+(x_2-x_3)^2+(x_3-x_1)^2 \quad ; \quad s_{yy} = (y_1-y_2)^2+(y_2-y_3)^2+(y_3-y_1)^2 $$ Then the second order moments of inertia / variances in the vertex case can be rewritten as:
$\sigma_{xx} = s_{xx}/9$ , $\sigma_{yy} = s_{yy}/9$ , $\sigma_{xy} = x_{xy}/9$ .
Compare this with the quantities of the flat plate case in the abovementioned paper . Then it turns out that the formulas are very similar :
$\sigma_{xx} = s_{xx}/36$ , $\sigma_{yy} = s_{yy}/36$ , $\sigma_{xy} = s_{xy}/36$ .
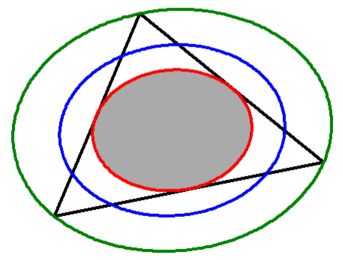
Which means that the ellipse in the vertex case is larger than the ellipse in the flat plate case, twice as large to be precise, because $\sqrt{36/9}=2$ . In the flate plate case, we get the Steiner Inellipse and in the vertex case, we get the Steiner Outellipse . For the slimness factor, this makes no difference.

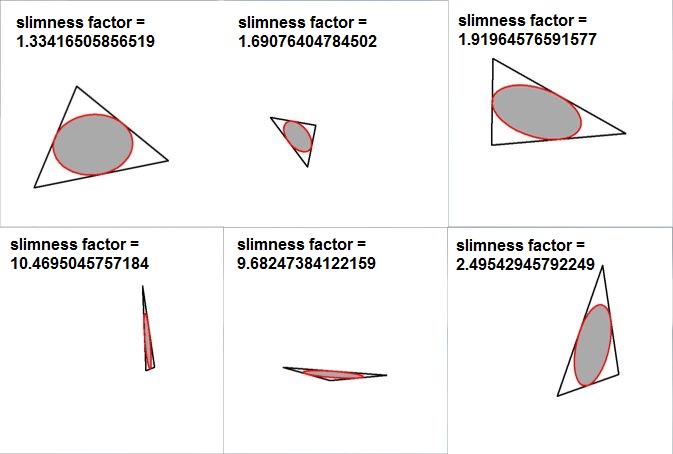
EDIT. Three Rods case. If I am right with my calculated ratio $3:6:12$ (instead of Matt's $3:8:12$) then we have the following picture for the $\color{green}{vertex}$ case, the $\color{blue}{rods}$ case and the flat $\color{red}{plate}$ case.
Conclusion: The slimness factor in all three cases is the same.

Coordinate independence. The formula for the Trace can be rewritten as follows: $$ \mbox{Tr} \sim (s_{xx}+s_{yy})/2 = (a^2+b^2+c^2)/2 $$ Where $a,b,c$ are the lengths of the triangle edges, as usual. The Determinant is conjectured to be proportional to the square of the area of the triangle. MAPLE is invoked to confirm this: 

A := simplify(s_xx*s_yy-s_xy^2);
B := simplify(((x_2-x_1)*(y_3-y_1)-(x_3-x_1)*(y_2-y_1))^2);
verify(A,3*B,equal);
                           true
Hence: $$ \mbox{Det} \sim (s_{xx}s_{yy}-s_{xy}^2) = 3(2A)^2 = 12 A^2 $$ Where $A$ denotes the Area of the triangle.

Quoting a comment: I don't see, where are the angles of the triangle in this formula?
With Heron's formula for the area $A$ and some algebra we find with the above: $$ \lambda_{\pm} \sim \frac{a^2+b^2+c^2}{2} \pm \sqrt{a^4+b^4+c^4-(a^2b^2+b^2c^2+a^2c^2)} $$ The sine rule says that, with one and the same proportionality constant $K$ : $$ a = K\sin(\alpha) \quad ; \quad b = K\sin(\beta) \quad ; \quad c = K\sin(\gamma) $$ Since in the (square root of) the quotient $\;\lambda_{+}/\lambda_{-}\;$ any proportionality constant will disappear, it is indeed possible to find a more "closed" formula for the Steiner based slimness factor, as a function of the angles only : simply replace $\;a,b,c\;$ by the corresponding $\;\sin(\alpha),\sin(\beta),\sin(\gamma)$ .