Quoted from Space-Time Approach to Quantum Electrodynamics
by R. P. Feynman, Phys. Rev. 76, 769 1949 :
We desire to make a modification of quantum electrodynamics analogous to the
modification of classical electrodynamics described in a previous article, A.
There the $\delta(s^2_{12})$ appearing in the action of interaction was replaced
by $f(s^2_{12})$ where $f(x)$ is a function of small width and great height.
My interpretation. According to a fundamental property of the Dirac-delta function:
$$
\int_{-\infty}^{+\infty} f(\xi) \delta(x-\xi)\, d\xi = \int_{-\infty}^{+\infty} \delta(\xi) f(x-\xi)\, d\xi = f(x)
$$
Now let $\delta(x)$ be replaced by a function $D_\sigma(x)$ that approximates
it as "a function of small width and great height". More precisely:
$$
\lim_{\sigma\to 0} D_\sigma(x) = \delta(x) \qquad \mbox{where} \qquad
\int_{-\infty}^{+\infty} D_\sigma(x) \, dx = 1
$$
Here $\sigma$ is the "small width" and the norm guarantees "great height". One-dimensional examples:
$$D_\sigma(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-x^2/(2\sigma^2)} \qquad \mbox{: Gaussian}$$
$$D_\sigma(x) = \frac{\sigma/\pi}{\sigma^2+x^2} \qquad \mbox{: Cauchy}$$
$$D_\sigma(x) = \left\{ \begin{array}{lll} 0 & \mbox{for} & x \le -\sigma \\
(\sigma+x)/\sigma^2 & \mbox{for} & -\sigma \le x \le 0 \\
(\sigma-x)/\sigma^2 & \mbox{for} & 0 \le x \le +\sigma \\
0 & \mbox{for} & +\sigma \le x \end{array} \right. \qquad \mbox{: Triangle}$$
$$D_\sigma(x) = \left\{ \begin{array}{lll} 0 & \mbox{for} & x \le -\sigma/2 \\
1/\sigma & \mbox{for} & -\sigma/2 \le x \le \sigma/2 \\
0 & \mbox{for} & +\sigma/2 \le x \end{array} \right. \qquad \mbox{: Rectangle}$$
The question is: can the replacement of $\,\delta\,$ by $\,D_\sigma\,$ be called Renormalization?
$$
\int_{-\infty}^{+\infty} f(\xi) D_\sigma(x-\xi)\, d\xi = \int_{-\infty}^{+\infty} D_\sigma(\xi) f(x-\xi)\, d\xi = \overline{f}(x)
$$
With other words: can $\overline{f}$ be called a renormalization of $f$ ?
The goal of Renormalization is that it must be capable of removing singularities.
Can our technique do that? The simplest example I can think of is two-dimensional -
which is typical: I couldn't find a decent one-dimensional example. Whatever might be the reason:
$$
f(r) = \frac{1}{r} \qquad ; \qquad D_\sigma(r) = \left\{ \begin{array}{lll} 1/(\pi \sigma^2) & \mbox{for} & r \le \sigma \\
0 & \mbox{for} & r > \sigma \end{array} \right.$$
Because by introducing polar coordinates we have $\,x = r\cos(\theta)\,$ and $\,y = r\sin(\theta)$ ;
$\,\xi = \rho\cos(\phi)\,$ and $\,\eta = \rho\sin(\phi)\,$
and $\,d\xi\,d\eta = \rho\,d\rho\,d\phi$ . Renormalization then goes as follows:
$$
f(r) = \frac{1}{r} \quad \Longrightarrow \quad
\overline{f}(r) = \iint D_\sigma(\sqrt{\xi^2+\eta^2}) \frac{d\xi d\eta}{\sqrt{(x-\xi)^2+(y-\eta)^2}} = \\
\frac{1}{\pi \sigma^2} \int_0^{2\pi} d\phi \int_0^\sigma \frac{\rho\,d\rho}{\sqrt{r^2+\rho^2-2r\rho\cos(\phi-\theta)}}
$$
But we only have to calculate $\,\overline{f}\,$ at the singularity $\,r=0$ , which simplifies the problem a whole lot:
$$ \overline{f}(0) = \frac{1}{\pi \sigma^2} \int_0^{2\pi} d \phi \int_0^\sigma d\rho = \frac{2}{\sigma} $$
It is seen that the singularity is indeed removed, that is: it is replaced by a number $2/\sigma$
which goes to infinity - as it should - if we only let $\sigma\to 0$ . But suppose that nobody wants the latter .. :-)
Update. Below is a (computer) sketch of functions involved with the example
for $\sigma=1$ and `xmin := 0; xmax := 5; ymin := 0; ymax := 5;` :
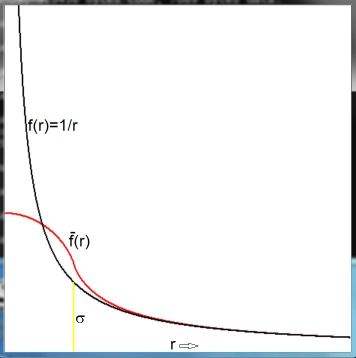
Update. Strangely enough, the "more difficult" renormalization
of the function $\sim 1/r^2$ in three dimensional space appears to be
less difficult than the abovementioned similar case in 2-D. See:
Self Energy Theory (PDF document).

