• Multigrid Calculus

Newton-Raphson algorithm

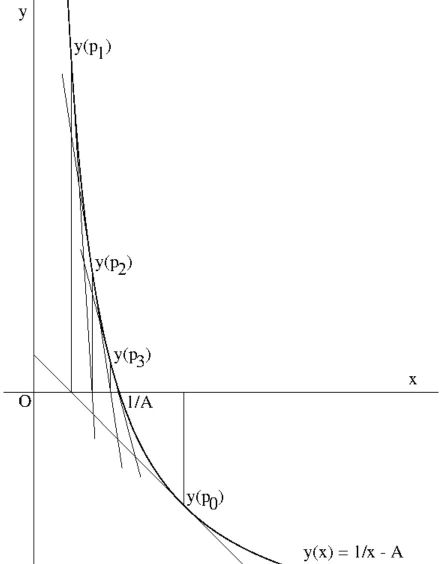
Thus by employing the Newton-Raphson algorithm, the inverse of a number can be found with quadratic speed, by performing solely additions and multiplications. Armed with this knowledge, let's make the transition from numbers to matrices. Determining the inverse of a matrix, filled with many numbers, seems to be much more like a challenge anyway.
Let the iterative process for matrices be defined by: $$ P_0 = I \quad \mbox{and} \quad P_{n+1} = 2.P_n - A.P_n.P_n $$ Here $I$ is the unity matrix, $A$ is the matrix to be inverted and $P_n$ are the successive iterands, which should converge to the inverse matrix $A^{-1}$.
Theorem. $$ \mbox{Let} \quad M = (I - A) \quad \mbox{or} \quad A = (I - M) \quad \mbox{then:} \quad P_n = (I - M^{2^n}) . A^{-1} $$ Proof by induction: $$ \begin{array}{lll} P_0 &=& I = A . A^{-1} = (I - M) . A^{-1} \\ P_{n+1} &=& \left(I - M^{2^{n+1}} \right) . A^{-1} \\ &=& \left(I - M^{2^n.2} \right) . A^{-1} \\ &=& \left[I - (M^{2^n})^2 \right] . A^{-1} \\ &=& \left(I - M^{2^n} \right) . \left(I + M^{2^n} \right) . A^{-1} \\ &=& \mbox{because all matrices are mutually commutative:} \\ &=& \left(I - M^{2^n} \right) . A^{-1} . \left[ 2.I - A.\left( I - M^{2^n} \right).A^{-1} \right] \\ &=& P_n.(2.I - A.P_n) = 2.P_n - A.P_n.P_n \end{array} $$ Let $m = 2^n$, then: $$ P_n = (I - M^m) . (I-M)^{-1} $$ For numbers, this would be the sum of a Geometric series : $$ (I - M^m).(I - M)^{-1} = (I + M + M^2 + M^3 + M^4 + M^5 + M^6 + ... + M^{m-1}) $$ For matrices, this Geometric Series turns out to be equivalent to an iterative "incremental Jacobi" solution method, as will not be futher explained here.
But there also does exist a product of terms, called the Euler expansion (don't remember where the naming comes from; a reference would be quite welcome): $$ (I - M^m).(I - M)^{-1} = \\ (I + M^{m/2}).(I - M^{m/2}).(I - M)^{-1} = \\ (I + M^{m/2}).(I + M^{m/4}).(I - M^{m/4}).(I - M)^{-1} = \\ (I + M^{m/2}).(I + M^{m/4}). \, ... \, (I+M^2).(I+M).(I-M).(I-M)^{-1} = \\ (I + M^{m/2}).(I + M^{m/4}). \, ... \, (I + M^8).(I + M^4).(I + M^2).(I + M) $$ Let the system of equations to be solved be given by $A.w = b$. Using the above sequences, we can write: $$ P_n = (I - M^{2^n}) . A^{-1} \quad \Longrightarrow \quad A^{-1} b = (I - M^{2^n})^{-1} . P_n b $$ $$ = (I - M^{2^n})^{-1} . (I + M^{m/2}).(I + M^{m/4}). \, ... \, (I + M^8).(I + M^4).(I + M^2).(I + M) b $$ Another way of looking at this is the following: $$ (I-M)^{-1} = (I-M)^{-1}.(I+M)^{-1}.(I+M) = (I-M^2)^{-1}.(I+M) = \\ (I-M^2)^{-1}.(I+M^2)^{-1}.(I+M^2).(I+M) = (I-M^4)^{-1}.(I+M^2).(I+M) $$ With other words: $$ w = (I-M)^{-1}.b = (I-M)^{-1}.(I+M)^{-1}.(I+M).b = (I-M^2)^{-1}.(I+M).b $$ Define $b := (I + M).b$ and $M := M^2$. Then again: $$ w = (I-M)^{-1}.b = (I-M)^{-1}.(I+M)^{-1}.(I+M).b = (I-M^2)^{-1}.(I+M).b $$ And this process can be repeated until we find a way to determine $(I-M)^{-1}$, preferrably without continuing the iterations ad infinitum.