Testable Predictions

From the thread "Update: Objections to Cantor's Theory". David Petry wrote:

Mathematics makes testable predictions.

From the thread "Han's startling new set theory". Han de Bruijn wrote:

I will choose my own example, 
preferrably one that you don't know anything about.

Jesse F. Hughes wrote:

if you want to change the subject, by all means, give it your best shot. 

But explicitness surely helps.  As I said before, one should expect 
that when you give an example of a testable prediction, you include a 
discussion of how to test these predictions and under what condition 
the prediction is verified and/or falsified.

The following is a revision of my original sci.math poster
as edited with Netscape's or Google's what_you_see_is_not_what_you_get_and_what_you_get_is_not_what_you_want.

Here is some Theory. Do not skip through. Read it. It is only 6 pages long and it's not quite difficult:

italiaan.pdf ( Fibonacci Iterations )

Though it's not exactly my style, I included the common Theorem + Proof sequences and even some rudimentary set theory as well. :-)
I have developed theory and practice from scratch within a week or so and would be glad to know if the material in this writeup contains any new insights.
If not so: where to find references to the same stuff?
Links to Fibonacci material are abundant even on the web. So it's very much probable, indeed, that my "discoveries" are not new altogether.

Maybe some of you are wondering why I find this stuff interesting. Well, it's a rather far-fetched purification of "how to solve large sets of linear equations resulting from a finite element method for regular meshes if such meshes become infinitely large" ... :-)

Here comes a computer program, which is the implementation of several Numerical Experiments, associated with the above Theory, of course:

italiaan.zip

Directions for use (Windows console application):

Make a subdirectory & go in there
Unzip (i.e. with pkunzip -d italiaan)
Run iterate(.exe = executable)
Follow instructions: 'iterate number'

Now, what are the Testable Predictions of our Theory, for the Numerical Experiments, to be carried out with the program ?

For values of 'number' equal to the Fibonacci Fractions F(k+1)/F(k) the iterands will become ill-conditioned at some place.
This is seen as '+/- oo' in the output (by catching the exception of a "zero" denominator).
Suggested experiments: iterate 1 ; iterate 2 ; iterate 1.5 ; iterate 1.66666666666 ; iterate 1.6 ; iterate 1.625 .
It is predicted that the first few iterates are Fibonacci Fractions in reverse order, until 1/1 .
Then the ill conditioning occurs and iterations will proceed from zero.
The 'number' values (1+sqrt(5))/2 and (1-sqrt(5))/2 are invariants. This is seen as lines of output which should be all the same.
Hint: you can copy and paste these values from 'iterate' without a numeric parameter. There is a difference, though. See below at (6).
Only numbers in the interval 1 < number < 2 can result in iterands which remain positive for a while.
Preferrably we should take an irrational number such as sqrt(2) or sqrt(3) , to check out without running into "infinities" by (1).
Hint: you can copy and paste these values from 'iterate' without a numeric parameter.
Any number > 2 results in a positive iterand < 1 . Any positive number < 1 results in negative iterands < -1 .
Any number that is negative results in iterands which are between -1 and 0 .
Summarizing: (2 < x < oo) → (0 < x < 1) → (-oo < x < -1) → (-1 < x < 0) . You can jump in anywhere.
As iterands become negative, they will oscillate around the value (1-sqrt(5))/2 . And converge to it.
More subtle. There is a difference if it comes to the invariants. The value (1-sqrt(5))/2 is stable while the value (1+sqrt(5))/2 is unstable.
The latter is worked out in a somewhat deviate experiment (: 70 iterations instead of the usual 20, for numbers close to that golden ratio).
Output shows that results are slowly shifting apart from (1+sqrt(5))/2 and nevertheless converge to (1-sqrt(5))/2 in the end.

The iterations in the " dangerous " interval 1 < x < 2 are worked out somewhat more extensively in the paper, by employing properties of intervals delineated by the Fibonacci Fractions F(k+1)/F(k) . But it isn't much more predictive nor is it more efficient than just carrying out the iterations. An experiment called 'frakties(.exe)' is included, though, in the package. It shows (graphically) how the sequence of Fibonacci Fractions quickly converges to the Golden Ratio.

Monday 19 September 2005. One, just one response so far ...

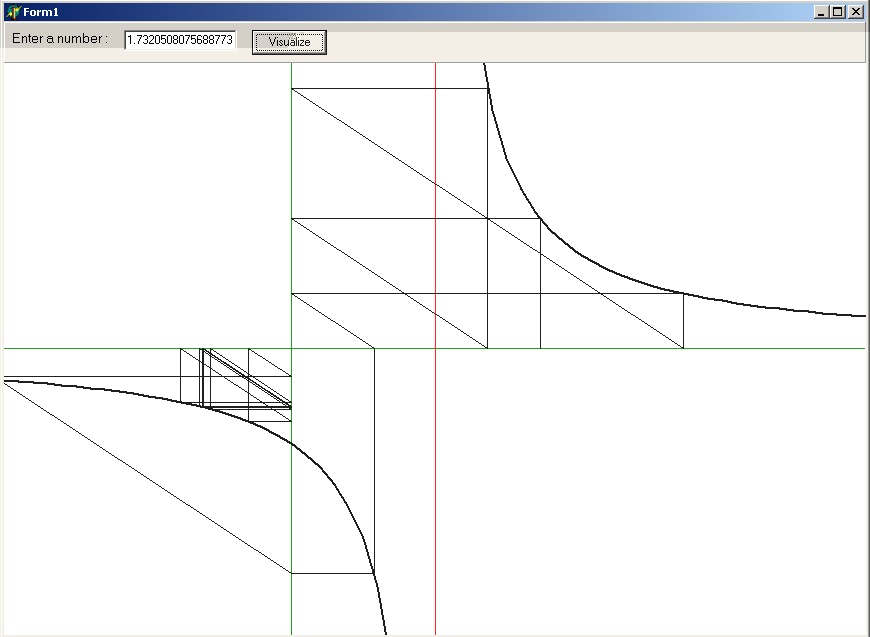
Last but not least: the usual picture that says more than a thousand words. It's a screen-shot of the executable 'grafisch', which is now included in the package for doing further numerical experiments.

Fibonacci Iterates