Schrikkelseconde

Processing math: 100%

Schrikkelseconde

Kritiek van Han de Bruijn
op Posts By: Wim De Jong

Volgens EVOSKEPSIS:

De aarde gaat steeds langzamer draaien. Daarom is tussen 1972 en 2015 al 25 keer een schrikkelseconde toegevoegd aan de officiële tijd. Terugrekenend moet de aarde 15 miljoen jaar geleden 100 keer harder gedraaid hebben dan nu, waardoor het leven dat we nu kennen er niet zou hebben kunnen bestaan

Hoe komt de auteur aan deze uitkomst? Laten we het proberen na te rekenen.
Veronderstellen we dat de rotatie snelheid van de aarde lineair afneemt in de tijd. Deze aanname wordt gerechtvaardigd doordat de de eb- en vloedbewegingen een constant negatief moment (

$M$ ) uitoefenen op de aarde en

$\,M \sim \dot{\omega}$ , dus de afgeleide van de hoeksnelheid

$\,\omega\,$ naar de tijd is constant. Het verband met de daglengte in seconden, de omwentelingsperiode

$\,T\,$ is :

$\omega = 2\pi / T$ . We kennen de afgeleide van de periode naar de tijd: deze is

$25/(2015-1972)$ seconden per jaar. Dus:

$\frac{dT}{dt} = 25/(2015-1972)/365/24/3600 = \mbox{het aantal seconden dat de dag per seconde langer duurt}$ Het verband met de hoeksnelheid is:

$\omega = \frac{2\pi}{T} \quad \Longrightarrow \quad \frac{d\omega}{dt} = -\frac{2\pi}{T^2}\frac{dT}{dt} = -\frac{2\pi}{(24\times3600)^2}\times 25/(2015-1972)/365/24/3600$ Hieruit kunnen we berekenen binnen welk tijdsbestek

$\,\Delta t\,$ de hoeksnelheid een factor 100 hoger was dan nu (denk aan lineair):

$100\times\omega-\omega = \Delta t \cdot \frac{2\pi}{(24\times3600)^2}\times 25/(2015-1972)/365/24/3600 \quad \Longrightarrow \\ \Delta t = 99\frac{2\pi}{(24\times 3600)} \times \frac{(24\times3600)^2}{2\pi \times 25/(2015-1972)/365/24/3600} \mbox{ sec} \quad \Longrightarrow \\ \Delta t = 99 \times 24 \times 3600 \times (2015-1972) / 25 \, \mbox{ jaar} \approx 15 \,\mbox{ miljoen jaar}$

Dit lijkt goed, maar het is FOUT!

Kernreferentie is Ephemeris time (Wikipedia):

Although ET is no longer directly in use, it leaves a continuing legacy. Its successor time scales, such as TDT [ Terrestrial Dynamical Time ] , as well as the atomic time scale IAT [ International Atomic Time ] (TAI) [ temps atomique international ] , were designed with a relationship that "provides continuity with ephemeris time". ET was used for the calibration of atomic clocks in the 1950s. Close equality between the ET second with the later SI second (as defined with reference to the cesium atomic clock) has been verified to within 1 part in $10^{10}$ .
The difference between ET and UT [ Universal Time ] is called $\Delta T$ ; it changes irregularly, but the long-term trend is parabolic, decreasing from ancient times until the nineteenth century, and increasing since then at a rate corresponding to an increase in the solar day length of 1.7 ms per century (see leap seconds).

Dit is in overeenstemming met Schrikkelseconde (Wikipedia):

Een schrikkelseconde is een seconde die aan de kalenderdatum/tijd toegevoegd wordt om het verschil in lengte tussen de gemiddelde zonnedag en de op de klok gebaseerde periode van precies 24 uur te corrigeren.
Sinds 1967 definieert men de precieze duur van de seconde met behulp van zogenoemde 'atoomklokken'. Hierbij gebruikt men straling met een bepaalde golflengte welke door een cesium-133 atoom wordt geabsorbeerd. De seconde is per definitie de duur van 9.192.631.770 periodes van deze straling.
De gemiddelde zonnedag is iets langer en neemt, als gevolg van een langzaam afnemende rotatiesnelheid van de aarde, ook geleidelijk toe (gemiddeld 1,7 ms per eeuw).

Wat andere internet referenties:

Waarom het zo omstreden is dat 2016 een seconde langer duurt
De aarde draait in een dag om zijn as. Een seconde is een dag gedeeld door 86.400. Maar die oude formule loopt niet helemaal gelijk met de atoomklokken die tegenwoordig worden gebruikt als referentie voor alle tijden op aarde. Een gemiddelde dag duurt 86.400,002 seconden. Dat komt neer op een seconde in anderhalf jaar tijd. Met een schrikkelseconde kan de aarde de atoomklok ‘achterhalen’. [ Atoomklokken lopen dus iets te snel / de tijd gemeten met een atoomklok is dus iets te lang ]
Schrikkelseconde komt met de schrik vrij
De aarde draait heel wispelturig rond: soms wat sneller, dan weer wat langzamer. Op de lange termijn is echter duidelijk te zien dat zijn draaisnelheid afneemt. Dat heeft verschillende oorzaken, bijvoorbeeld door getijdenwerking van de maan of het smelten van poolijs. Als poolijs smelt en water naar de evenaar stroomt remt dit de aarde af, net als wanneer een kunstschaatser zijn armen uitstrekt tijdens een pirouette. [ .. ] Normaliter vinden schrikkelseconden eind juni of eind december plaats. [ Zoals te zien is in onderstaande grafiek ]
Wat als .. de aarde stopt met draaien
Voor de totstandkoming van de maan zouden de dagen op onze planeet slechts twee tot drie uur lang zijn geweest. [ .. ] Over zo’n 100 jaar is een dag op aarde ongeveer 2 milliseconden korter dan nu het geval is. [ Er zal wel "langer" bedoeld zijn en ook $2 \approx 1,7$ milliseconden. Dan klopt het met hierboven ]
Leap Seconds
Half a billion years ago (when the Earth was 4 billion years old, instead of 4.5), each day was 22 hours long instead of 24.
[ Want $\,500.000.000/100 \times 1.7/1000/3600 = 50\times 1.7/36 \approx 2.36$ uur korter ]
Duurden de dagen vroeger net zo lang als nu?
Goed nieuws dus, zij het in de categorie dode mus: pas over 50.000 jaar zal een dag gemiddeld één seconde langer duren dan nu.
[ Want $\,50.000/100 \times 1.7/1000 = 0.5 \times 1.7 \approx 0.85$ seconden ]
Day length fluctuations
Grafiek ook bewaard als (BMP en) JPG:

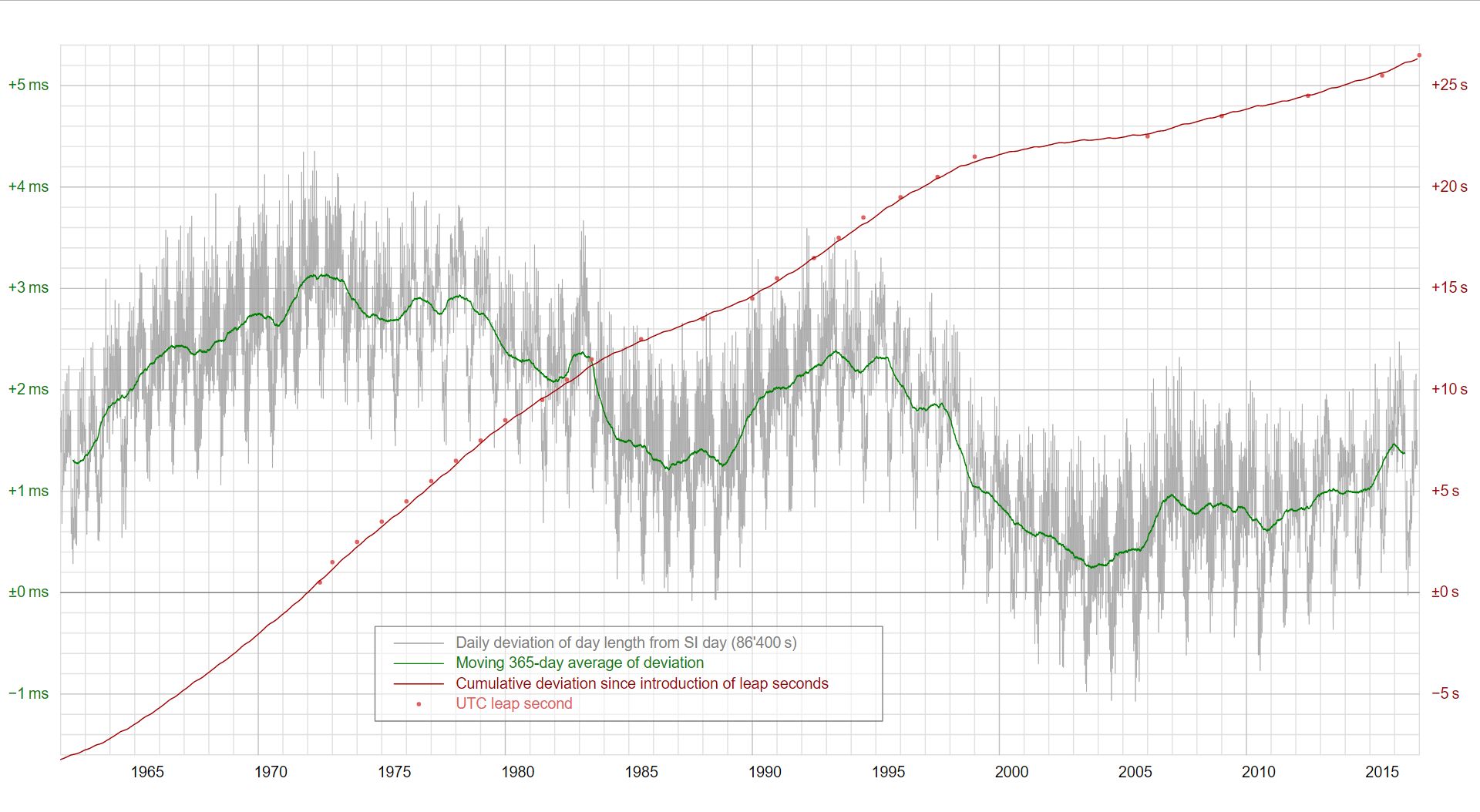
Als de atoomtijd

$\,t\,$ in 1972 correct gesynchroniseerd zou zijn geweest met de zonnedag-tijd

$\,\color{red}{T(t)}$ , dan zou men ter plaatse een horizontale raaklijn verwachten :

$\,t = T = 1972\,$ en

$\,dT/dt(1972) = 0$ . Dit is echter niet het geval. Reeds in 1972 duurt de dag zoals gemeten met de atoomklok systematisch 0.002 seconden langer dan normaal. Hetgeen per jaar neerkomt op

$365 \times 0.002 \approx 0.73$ seconden. En dit heeft dus niets te maken met de afnemende draaisnelheid van de aarde om zijn as. Corrigerend voor deze systematische fout in de atoomtijd versus zonnedag-tijd komt men kennelijk uit op 1,7 ms per eeuw als werkelijke waarde voor de afnemende daglengte. In onze berekening komt er dan:

$\frac{dT}{dt} = 1.7/1000/100/365/24/3600 = \mbox{het aantal seconden dat de dag per seconde langer duurt}$ In plaats van de andere waarde hierboven. En dat maakt in die 15 miljoen jaar een enorm verschil:

$n\cdot\omega-\omega = (15,000,000 \times 365 \times 24 \times 3600) \cdot \frac{2\pi}{(24\times3600)^2}\times 1.7/1000/100/365/24/3600 \quad \Longrightarrow \\ n = 1 + \frac{24 \times 3600}{2\pi}\cdot (15,000,000 \times 365 \times 24 \times 3600) \cdot \frac{2\pi}{(24\times 3600)^2}\times 1.7/1000/100/365/24/3600 \\ = 1 + 0.002951389 \approx 1.003$ Een verschil van drie pro mille. De omwentelingssnelheid van toen is dus nauwelijks te onderscheiden van de huidige omwentelingssnelheid. De conclusie is helder:

De aarde gaat steeds langzamer draaien. Daarom is tussen 1972 en 2015 al 25 keer een schrikkelseconde toegevoegd aan de officiële tijd. Terugrekenend moet de aarde 15 miljoen jaar geleden 100 keer harder gedraaid hebben dan nu, waardoor het leven dat we nu kennen er niet zou hebben kunnen bestaan. [ Inmiddels is deze zinsnede door de auteur van EVOSKEPSIS gewijzigd. Echter de "draaisnelheid pakweg 100 keer hoger" blijft mijns inziens volkomen uit de lucht gegrepen: zie onder ]

Maar laat ons 500 miljoen jaar geleden nemen. Het is niet nodig om de berekening helemaal over te doen. We hoeven een deel van de vorige uitkomst slechts te vermeningvuldigen met

$\,500/15$ :

$n = 1 + 0.002951389 \times 500/15 = 1.0983766 \quad \Longrightarrow \quad \mbox{dag } = 24/1.0983766 = 21.85 \mbox{ uur}$ Hiermee is de zonnedag lengte, inderdaad, ongeveer 22 uur (zie boven). Dit bevestigt de juistheid van onze rekenwijze.
Vier en een half miljard jaar is volgens de seculiere wetenschap de ouderdom van de aarde. Op dezelfde manier vinden we dan:

$n = 1 + 0.002951389 \times 4500/15 = 1.8854167 \quad \Longrightarrow \quad \mbox{dag } = 24/1.8854167 = 12.73 \mbox{ uur}$ Dus toen draaide de aarde ongeveer twee keer zo snel als nu. Dit is echter zwaar theoretisch: meestal mag niet worden aangenomen dat een extrapolatie over zo'n lange tijd nog steeds lineair is. Nog wat internet referenties:

Afgezien van dit alles, de schrikkelseconde is een waar wespennest, zoals wel blijkt uit de volgende discussie op een Wetenschapsforum : vertraging aardrotatiesnelheid..hoe groot? .