De energiedichtheid $u$ in het elektrische veld van een puntlading $q$ wordt
gegeven door $ u = \frac{1}{2} \epsilon_0 E^2 $ waarbij het elektrische veld $E$ op
een afstand $r$ wordt gegeven door: $$ E = \frac{q}{4 \pi \epsilon_0 r^2} $$
Hierin is $\epsilon_0 = 8,854187817\times 10^{-12}\; C^2 m^{-2} N^{-1}$ .
De totale energie in het veld wordt gegeven door de integraal van de energiedichtheid $u$
over de ruimte:
$$ U = \iint u \, dV = \int_0^\infty\frac{1}{2}\epsilon_0 \left(\frac{q}{4\pi\epsilon_0 r^2}
\right)^2 4 \pi r^2 dr \ =
\frac{q^2}{8 \pi \epsilon_0} \int_0^\infty \frac{dr}{r^2} =
\frac{q^2}{8 \pi \epsilon_0} \left[ \frac{1}{r} \right]_0^\infty = \infty $$
Er is dus een oneindige uitkomst voor de eigen energie van het elektron. Zoals bekend
is dit een ernstig probleem in de klassieke elektrodynamica. Zo voorspelt de theorie
dat een elektron niet kan bewegen. Einstein's formule luidt immers: $U=mc^2$ (hier niet
$E=mc^2$ omdat bij ons de letter $E$ staat voor elektrische veldsterkte). Hiermee is de massa
van het elektron oneindig en een oneindig grote massa kan niet in beweging worden gebracht.
Maar .. er is reden om aan te nemen dat een elektron geen duidelijk bepaalde positie heeft.
Om te beginnen is er de Zitterbewegung.
Volgens deze theorie fluctueert een elektron met de snelheid van het licht en met
een amplitude gelijk aan de Compton golflengte om zijn (rust)positie.
Dezelfde Compton golflengte komt ook
tevoorschijn bij de volgende beschouwing. Stel dat men bijvoorbeeld probeert om een elektron
waar te nemen met een lichtmicroscoop, zoals hieronder geschetst:
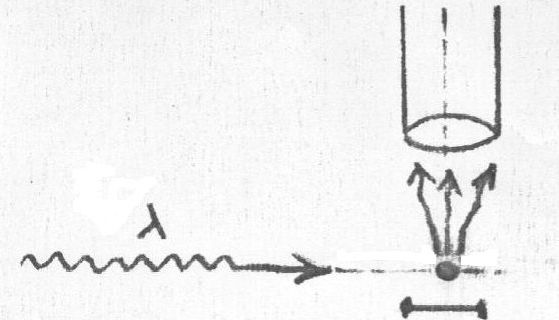dan treedt het zogenaamde
Compton-effect op:
$$
\delta\lambda = \lambda'-\lambda = \frac{h}{m c}(1-\cos\theta) =
\frac{h}{m c} \approx 2.4263102389(16)\times 10^{-12}\, m
$$
Het laatste omdat het elektron zich recht onder de microscoop bevindt, en dus $\;\theta = \pi/2\;
\Longrightarrow\; (1-\cos\theta)=1$ . Dit betekent dat men met een lichtmicroscoop nooit verder
kan komen dan een onzekerheid $\;h/(m c)\;$ in de plaatsbepaling van het elektron. Puur theoretisch
overigens, een zogenaamd Gedachte-experiment, want in werkelijkheid zal men nooit een elektron op deze manier
kunnen waarnemen.
Inderdaad kan het probleem van de oneindige zelf-energie
van het elektron worden opgelost door een onnauwkeurigheid in de positie van het elektron
aan te nemen. Of een onnauwkeurigheid in het vaststellen van de afstand tot het elektron.
Het maakt niet uit. In beide gevallen geldt, wanneer wordt uitgegaan van de eenvoudigste
manier van berekenen:
$$
\tilde{r} = r \pm \sigma \quad \mbox{met} \quad \sigma \approx \frac{h}{m c} \quad \mbox{?}
$$
Hierin is $\sigma$ de onnauwkeurigheid.
In de noemer van de formule voor de veldsterkte $E$ komt de oppervlakte van een bol voor :
$4\pi r^2$ . Deze wordt nu $\;4\pi\tilde{r}^2$ . De gemiddelde oppervlakte is dan:
$$
4\pi\overline{r^2} = 4\pi \frac{(r-\sigma)^2+(r+\sigma)^2}{2} =
4\pi \frac{(r^2-2r\sigma+\sigma^2)+(r^2+2r\sigma+\sigma^2)}{2} =
4\pi (r^2+\sigma^2)
$$
Maar dit is misschien wat kort door de bocht. Een meer correcte beschouwingswijze zou uit kunnen
gaan van de in de statistiek zeer gebruikelijke normale verdeling
Dit geeft echter precies dezelfde uitkomst als we op de eenvoudige manier hebben gevonden!
Vervang nu in de wet van Coulomb $r^2$ door $\overline{r^2} = r^2+\sigma^2$ .
Dit drukt uit dat er een onzekerheid is in de afstand en dat deze doorwerkt in
de uitdrukking voor het boloppervlak in de noemer van de natuurwet. Het resultaat is
een zogenaamde Cauchy verdeling; deze is voor redelijke afstanden $r >> \sigma$
niet te onderscheiden van een Coulomb veldsterkte. Dit levert voor de gemiddelde veldenergie:
$$
\overline{U} = \int_0^\infty\frac{1}{2}\epsilon_0 \left[
\frac{q}{4\pi\epsilon_0 (r^2+\sigma^2)}\right]^2 4 \pi r^2\, dr
= \frac{q^2}{8 \pi \epsilon_0} \int_0^\infty \frac{r^2\,dr}{(r^2+\sigma^2)^2}
$$
Berekenen we eerst een onbepaalde integraal:
$$
\int \frac{r^2\,dr}{(r^2+\sigma^2)^2} =
\int \frac{r\,d\left[\frac{1}{2}(r^2+\sigma^2)\right]}{(r^2+\sigma^2)^2} =
-\frac{1}{2}\int r\,d\left(\frac{1}{r^2+\sigma^2}\right) =
-\frac{1}{2}\frac{r}{r^2+\sigma^2} + \frac{1}{2}\int\frac{dr}{r^2+\sigma^2} =\\
-\frac{1}{2}\frac{r}{r^2+\sigma^2} + \frac{1}{2\sigma}\int\frac{d(r/\sigma)}{1+(r/\sigma)^2} =
-\frac{1}{2}\frac{r}{r^2+\sigma^2} + \frac{1}{2\sigma}\arctan\left(\frac{r}{\sigma}\right)
$$
En vervolgens de bepaalde integraal:
$$
\int_0^\infty \frac{r^2\,dr}{(r^2+\sigma^2)^2} =
-\frac{1}{2}\left[\frac{r}{r^2+\sigma^2}\right]_0^\infty
+ \frac{1}{2\sigma}\left[\arctan\left(\frac{r}{\sigma}\right)\right]_0^\infty =
0 + \frac{1}{2\sigma}\frac{\pi}{2}
$$
De singulariteit in de oorsprong is hiermee verwijderd, want we krijgen het volgende
eenvoudige, maar vooral eindige resultaat:
$$ \overline{U}
= \frac{q^2}{8 \pi \epsilon_0} \frac{1}{4}\frac{\pi}{\sigma}
= \frac{q^2}{32\,\epsilon_0\sigma}
$$
De uitkomst moet gelijk zijn aan $m c^2$, dus we berekenen voor de straal van het elektron:
$$
\sigma = \frac{q^2}{32\,\epsilon_0 m c^2} =
\frac{1}{4\pi\epsilon_0}\frac{q^2}{m c^2}\frac{\pi}{8} = \frac{\pi}{8}r_e \approx 0.39 \times r_e
$$
Hierin is $r_e$ de klassieke elektron-straal $\approx 2,8179403267(27)\times 10^{-15}\,m$ :
Classical electron radius .
Onze schatting ligt in dezelfde orde van grootte: $\sigma \approx 1,107\times 10^{-15}\,m$ ; dit is
meer dan tweeduizend keer zo klein als de Compton golflengte.
Er bestaat ook een (minder uitgebreid)
Engelstalig equivalent van dit artikel.