overzicht overview
Fuzzy Optics [ NL ]
Sometimes you can see things better with your eyes half shut. Maybe there
is no more lucid way than this for expressing the idea of continuity.
In the physics lessons at school, a little piece of geometric optics has always
been part of the program: convex and concave mirrors and lenses. Herewith it is
assumed, quite naturally, that any image of an object is crisp and clear.
My proposal here is to say goodbye to this good habit, and pay attention to
fuzzy images instead. In the figure below, much enlarged, we see the
geometry of such a fuzzy image:
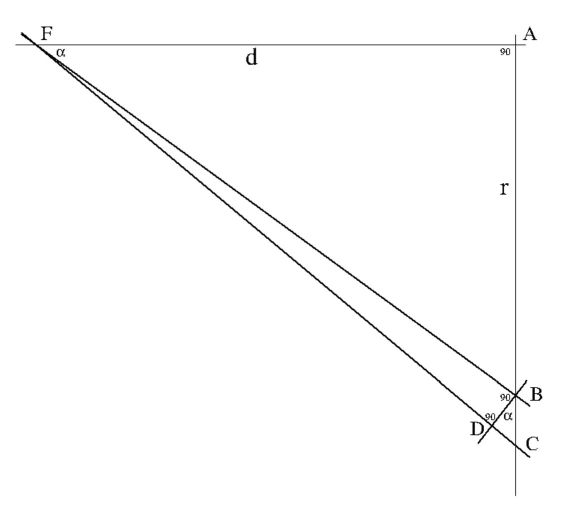
Usually, a crisp image is formed at the spot $F$. However, now suppose that the
image plane is shifted a little bit to the right, over a distance $d$ .
Consider a very narrow light bundle $FBC$. The bundle fans out slowly and
hits the image plane at $BC$. Because the bundle is very narrow, both the
angles $FBD$ and $FDB$ are approximately 90 degrees. This means that the angle
$CBD$ will be approximately equal to the angle $BFA$. Name this angle $\alpha$.
The light density $P$ at the surface $BC$ shall be calculated. Assume that the
light is emitted by a point source with strength $1$, then:
$P=cos(\alpha)/(2\pi R^2) $ (: half sphere).
Here $cos(\alpha) = d/R$ and $R = \sqrt{r^2+d^2} $. If the surface $BC$ is
contracted to a point, then we find for the light strength in place the
following "exact" expression:
$$ P(r) = \frac{d/(2\pi)}{(r^2+d^2)^{3/2}} $$
It is noted that the derivation with help of the approximately straight angles
$FBD$ and $FDB$ is motivated only afterwards, as the limit "has been taken".
This is a typical example of a "derivation with pain", as it is applied quite
frequently in the applied sciences / physics.
A few things are noted. At first that a crisp image is obtained (a delta
function to be precise) as soon as the distance $d$ approaches zero.
Integration of the formula over the whole image plane obviously must yield a
total amount of light equal to $1$ . This can be checked out:
$$ \iint \frac{d/2\pi}{(r^2+d^2)^{3/2}} \, r.dr.d\phi =
2\pi.\frac{1}{2\pi}.\int_0^\infty \!
\frac {r/d.d(r/d)} {\left[(r/d)^2+1\right]^{3/2} } =
- \frac{2}{2}.\left[x^{-1/2}\right]_1^\infty = 1 $$
If a straight line is considered, instead of a point-like light source, then the
function $P$ must be integrated all over this line. Along the line, measurement
is defined with a length $l$. The radius $r$ in the above formulas is replaced
by $p^2+l^2$, where $p$ is the distance of the point $(x,y)$ to the line. The
integration procedure therefore is as follows:
$$ L = \int_{-\infty}^{+\infty} \! \frac{d/2\pi}{(p^2+l^2+d^2)^{3/2}} \, dl =
\frac{d/2\pi}{p^2+d^2} \int_{-\infty}^{+\infty} \!
\frac{d\left( \frac{l}{\sqrt{p^2+d^2}} \right)}
{ \left[ 1 + \left( \frac{l}{\sqrt{p^2+d^2}} \right)^2 \right]^{3/2} } $$
$$ = \frac{d/2\pi}{p^2+d^2}
\left[ \frac{x}{(1+x^2)^{1/2}} \right]_{-\infty}^{+\infty}
= \frac{d/2\pi}{p^2+d^2} . 2 $$
If the equation of the line is given by $ ax + by + c = 0 $ , then the distance
$p$ of a point $(x,y)$ to this line is given by a well-known formula as
$ p = (ax + by + c)/\sqrt(a^2+b^2) $. Herewith the light strength of a fuzzy
image of a line is given by:
$$ L(x,y) = \frac{d/\pi}{(ax+by+c)^2/(a^2+b^2)+d^2} $$
This function is known from statistics as a Cauchy distribution. Again,
for $d \rightarrow 0$ , a crisp picture is obtained and the integral strength
of the light is still equal to unity.
