DriehoeksAlgebra
Laten we eerst gaan kijken naar de eenvoudigste niet-triviale elementvorm in
twee dimensies: de lineaire driehoek.
Het gedrag van een funktie wordt binnen een driehoek benaderd door een
lineaire interpolatie tussen de funktie-waarden op de hoekpunten. Hoekpunten
die meestal ook dienen als knooppunten: punten waarop diverse driehoeken
in een eindige elementen mesh aan elkaar, en aan andere elementen worden
vastgeknoopt. Laat $T$ een willekeurige funktie zijn, lineair geïnterpoleerd
tussen de knooppuntswaarden, en $x,y$ vlakke cartesische coördinaten, dan is
er een lineair verband:
$$
T = A.x + B.y + C
$$
Waarin de konstanten $ A,B,C $ nog nader bepaald dienen te worden.
Substitueer $ x=x_k $ and $ y=y_k $ met $ k=1,2,3 $:
$$
\left[ \begin{array}{c} T_1 \\ T_2 \\ T_3 \end{array} \right] =
\left[ \begin{array}{ccc} 1 & x_1 & y_1 \\
1 & x_2 & y_2 \\
1 & x_3 & y_3 \end{array} \right]
\left[ \begin{array}{c} C \\ A \\ B \end{array} \right]
$$
Om te beginnen is:
$$
T_1 = A.x_1 + B.y_1 + C
$$
De eerste van deze vergelijkingen kan dus reeds gebruikt worden om de constante
$C$ eens en voor altijd te elimineren:
$$
T - T_1 = A.(x - x_1) + B.(y - y_1)
$$
De constanten $A$ en $B$ worden nu bepaald door:
$$
\begin{array}{ll}
T_2 - T_1 = A.(x_2 - x_1) + B.(y_2 - y_1) \\
T_3 - T_1 = A.(x_3 - x_1) + B.(y_3 - y_1)
\end{array}
$$
Twee vergelijkingen met twee onbekenden. De oplossing wordt gevonden met de
regel van Cramer. Kennis van lineaire algebra is onmisbaar bij het omgaan met
zaken in de Numerieke Wiskunde, maar in dit eenvoudige geval kan het ook op de
volgende manier. Zorg dat de bovenste vergelijking wordt vermenigvuldigd met
$(y_3 - y_1)$, de onderste met $(y_2 - y_1)$. Aftrekken elimineert dan $B$.
Insgelijks wordt $A$ geëlimineerd door vermenigvuldigen met respektievelijk
$(x_3 - x_1)$ en $(x_2 - x_1)$. Het resultaat is:
$$
\begin{array}{ll}
A = [ (y_3 - y_1).(T_2 - T_1) - (y_2 - y_1).(T_3 - T_1) ] / \Delta \\
B = [ (x_2 - x_1).(T_3 - T_1) - (x_3 - x_1).(T_2 - T_1) ] / \Delta
\end{array}
$$
Er bestaan verschillende manieren om de determinant $\Delta$ te schrijven. Het is
handig als men zich sommige vormen weet te herinneren, als dat zo te pas komt:
\begin{eqnarray*}
&& \Delta = (x_2 - x_1).(y_3 - y_1) - (x_3 - x_1).(y_2 - y_1) \\
&& \Delta = 2 \times \mbox{ oppervlakte driehoek } \\
&& \Delta = x_1.y_2 + x_2.y_3 + x_3.y_1 - y_1.x_2 - y_2.x_3 - y_3.x_1 \\
&& \Delta = x_1.(y_2 - y_3) + x_2.(y_3 - y_1) + x_3.(y_1 - y_2) \\
&& \Delta = y_1.(x_3 - x_2) + y_2.(x_1 - x_3) + y_3.(x_2 - x_1) \\
&& \Delta = \left\| \begin{array}{ccc} 1 & x_1 & y_1 \\
1 & x_2 & y_2 \\
1 & x_3 & y_3 \end{array} \right\|
\end{eqnarray*}
Hoe het ook zij, uit het bovenstaande kan men konkluderen dat:
$$
T - T_1 = \xi.(T_2 - T_1) + \eta.(T_3 - T_1)
$$
Hierin is:
$$
\begin{array}{ll}
\xi = [ (y_3 - y_1).(x - x_1) - (x_3 - x_1).(y - y_1) ] / \Delta \\
\eta = [ (x_2 - x_1).(y - y_1) - (y_2 - y_1).(x - x_1) ] / \Delta
\end{array} $$
Of: $$
\left[ \begin{array}{c} \xi \\ \eta \end{array} \right] =
\left[ \begin{array}{cc} + (y_3 - y_1) & - (x_3 - x_1) \\
- (y_2 - y_1) & + (x_2 - x_1)
\end{array} \right] / \Delta
\left[ \begin{array}{c} x - x_1 \\ y - y_1 \end{array} \right]
$$
Herkenbaar is de inverse van het volgende probleem:
$$
\left[ \begin{array}{c} x - x_1 \\ y - y_1 \end{array} \right] =
\left[ \begin{array}{cc} (x_2 - x_1) & (x_3 - x_1) \\
(y_2 - y_1) & (y_3 - y_1)
\end{array} \right]
\left[ \begin{array}{c} \xi \\ \eta \end{array} \right] $$
Of: $$
\begin{array}{ll}
x - x_1 = \xi .(x_2 - x_1) + \eta.(x_3 - x_1) \\
y - y_1 = \xi .(y_2 - y_1) + \eta.(y_3 - y_1)
\end{array} $$
Maar we vonden in eerste instantie ook:
$$
T - T_1 = \xi .(T_2 - T_1) + \eta.(T_3 - T_1)
$$
We zien dat precies dezelfde uitdrukking opgaat voor zowel de funktie $T$
als voor de coördinaten $x$ en $y$. Hiermee is uitgelegd wat men pleegt te
verstaan onder een isoparametrische ("zelfde parameters") transformatie.
Isoparametrische transformaties zullen we nog een aantal malen tegenkomen.
Refererend aan de formules welke $\xi$ en $\eta$ uitdrukken in $x$ en $y$:
$$ \begin{array}{ll}
\xi = [ (y_3 - y_1).(x - x_1) - (x_3 - x_1).(y - y_1) ]/\Delta \\
\eta = [ (x_2 - x_1).(y - y_1) - (y_2 - y_1).(x - x_1) ]/\Delta
\end{array} $$
Dus $\xi$ kan worden geïnterpreteerd als: oppervlakte van de deel-driehoek
welke wordt opgespannen door de vectoren $ (x - x_1 , y - y_1) $ en
$ (x_3 - x_1 , y_3 - y_1) $, gedeeld door de oppervlakte van de driehoek als
geheel.
En $\eta$ kan worden geïnterpreteerd als: oppervlakte van de deel-driehoek
welke wordt opgespannen door de vectoren $ (x - x_1 , y - y_1) $ en
$ (x_2 - x_1 , y_2 - y_1) $, gedeeld door de oppervlakte van de driehoek als
geheel.
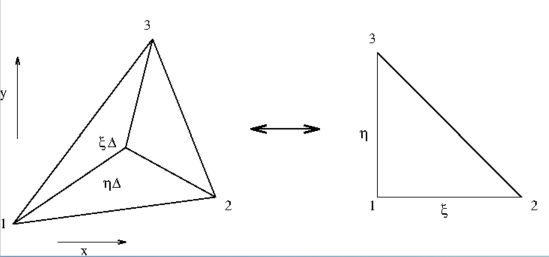
Dit is de reden waarom $ \xi $ en $ \eta $ wel oppervlakte-coördinaten
worden genoemd: zie bovenstaande figuur. Hierin is (twee keer) de oppervlakte
van de driehoek als geheel aangeduid met $\Delta$.
Er bestaan zelfs drie van deze coördinaten in de litteratuur [OC].
De derde oppervlakte-coördinaat is natuurlijk afhankelijk van de andere twee,
en gelijk aan $(1-\xi-\eta)$.
In plaats van te spreken over oppervlakte-coördinaten, geven wij de voorkeur
aan de benaming lokale coördinaten $\xi$ en $\eta$ van een element,
dit in tegenstelling tot de globale coördinaten $x$ en $y$.
Het is mogelijk dat lokale coördinaten overeenkomen met globale coördinaten.
Een driehoek waarvoor dit het geval is wordt een moeder-element (Engels:
parent element) genoemd. De beeltenis van zo'n moeder-element vindt men evenzo
in bovenstaande figuur: het is een gelijkbenige rechthoekige driehoek.
Beschouw nogmaals de uitdrukking:
$$
T - T_1 = \xi .(T_2 - T_1) + \eta.(T_3 - T_1)
$$
Partieel differentieren naar $ \xi $ en $ \eta $ geeft:
$$
\partial T/\partial \xi = T_2 - T_1 \quad ; \quad \partial T/\partial \eta = T_3 - T_1
$$
Dus: $$
T = T(0) + \xi \frac{\partial T}{\partial \xi} + \eta \frac{\partial T}{\partial \eta}
$$
Dit is een stuk van de Taylorreeks-ontwikkeling van $T(\xi,\eta) $ rondom (1).
Zulke Taylorreeks-ontwikkelingen komen erg vaak voor in de eindige differentie
analyse. Schrijf anderszins als volgt:
$$
T = (1 - \xi - \eta ).T_1 + \xi.T_2 + \eta.T_3
$$
De funkties $ (1-\xi-\eta) , \, \xi , \, \eta $ noemt men de vormfunkties
(Engels: shape functions) van het Eindige Element. Vormfunkties $N_k$ hebben de
eigenschap dat ze één zijn in een van de hoekpunten (k) en nul in alle andere
hoekpunten. In ons geval zijn de vormfunkties:
$$
N_1 = 1-\xi-\eta \quad ; \quad N_2 = \xi \quad ; \quad N_3 = \eta
$$
We hebben nu dus twee representaties, die bijna trivialiter hetzelfde zijn:
$$ \begin{array}{ll}
T = T_1 + \xi.(T_2 - T_1) + \eta.(T_3 - T_1) \quad
& \mbox{: Eindige Differenties} \\
T = (1 - \xi - \eta).T_1 + \xi.T_2 + \eta.T_3 \quad
& \mbox{: Eindige Elementen}
\end{array} $$
Wat voor termen kan men diskretizeren op het domein van een lineaire driehoek?
In de eerste plaats de funktie $T(x,y)$ zelf natuurlijk. Maar men kan ook een
poging ondernemen voor de partiële afgeleiden $\partial T/\partial x$ en $\partial T/\partial y$.
Gebruik makend van het bovenstaande, vinden we:
$$ \begin{array}{ll}
\partial T/\partial x = A = [ (y_3 - y_1).(T_2 - T_1) - (y_2 - y_1).(T_3 - T_1) ]/\Delta \\
\partial T/\partial y = B = [ (x_2 - x_1).(T_3 - T_1) - (x_3 - x_1).(T_2 - T_1) ]/\Delta
\end{array} $$
Door termen behorend bij dezelfde knooppuntswaarden $T_k$ bijeen te nemen, kan
dit ook worden geschreven als:
$$
\Delta \left[ \begin{array}{c} \partial T/\partial x \\ \partial T/\partial y \end{array} \right] =
\left[ \begin{array}{ccc} +(y_2 - y_3) & +(y_3 - y_1) & +(y_1 - y_2) \\
-(x_2 - x_3) & -(x_3 - x_1) & -(x_1 - x_2) \end{array}
\right] \left[ \begin{array}{c} T_1 \\ T_2 \\ T_3 \end{array} \right]
$$
Of, in de vorm van een Operator:
$$
\left[ \begin{array}{c} \partial/\partial x \\ \partial/\partial y \end{array} \right] =
\left[ \begin{array}{ccc} +(y_2 - y_3) & +(y_3 - y_1) & +(y_1 - y_2) \\
-(x_2 - x_3) & -(x_3 - x_1) & -(x_1 - x_2) \end{array}
\right] / \Delta $$
Het rechterlid zal in het vervolg Differentiatie Matrix worden genoemd;
de term is afkomstig van Csendes [ZJ].
Hiermee kunnen we zeggen dat de gradiënt-operator, op een lineaire driehoek,
wordt gerepresenteerd door een $2 \times 3$ differentiatie matrix.
