 2 :
2 :  3 :
3 : 
1kg , 500 g , 2 x 200 g , 100 g , 50 g , 2 x 20 g , 10 g , 5 g , 2 x 2 g, 1 g , 500mg , 2 x 200mg , 100mg , 50mg , 2 x 20mg , 10mg

Decimal calibration is not what we are looking for indeed. The reason is simple: it's rather bothersome to manufacture these weights at home. We would like to suggest a much more feasible alternative: printing {\em paper}.
Paper, here in Europe at least, comes standard as $A4$. The weight is usually known: $75g/m^2$ is read here for common printer paper. Sixteen of these $A4$ form an $A0$ size paper, with area $ = 1 m^2$ (sic, why would that be?) and hence a weight of $75g$. Which by the way is not an unreasonable weight to start with. Eight $A4$ form an $A1$ size, Four $A4$ make an $A2$. Two $A4$ make an $A3$. But by far the greatest advantage is that it's very easy to fold one $A4$ and make two $A5$ of it, fold one $A5$ and make two $A6$ of it, fold one $A6$ and make two $A7$ of it, fold one $A7$ and make two $A8$ of it, fold one $A8$ and make two $A9$ of it (we only need one of those two). Okay, that seems to be enough for our purpose. What has been accomplished now is that we have a collection of ten "calibrated" weights, non-decimal, {\em binary} weights to be precise. A picture says more than a thousand words: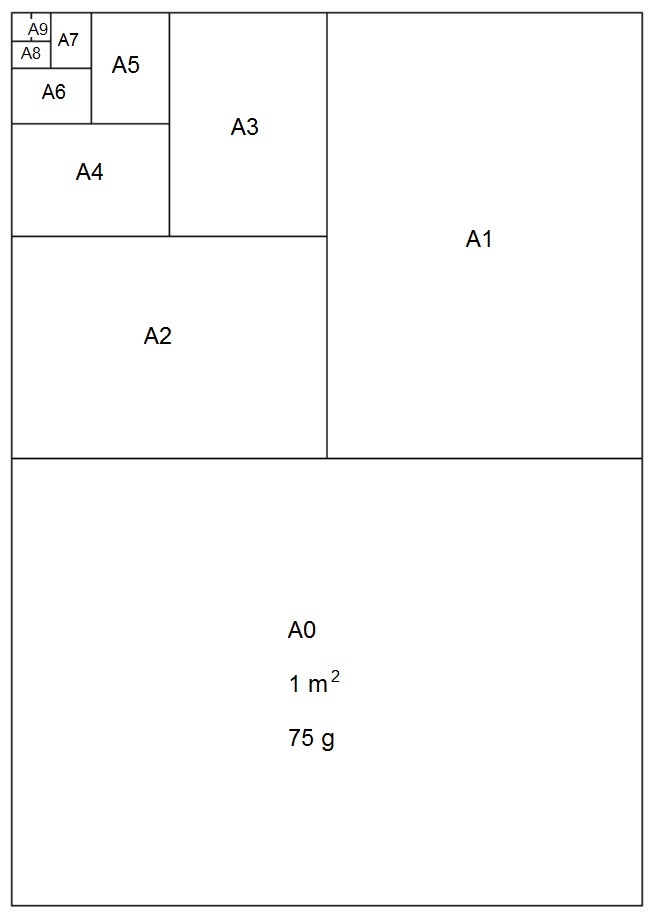
1 :  2 :
2 :  3 :
3 : 
A0 A1 A2 A3 A4 A5 A6 A7 A8 A9
4 :  5 :
5 :  6 :
6 : 
A0 A1 A1 A2
7 :  8 :
8 :  9 :
9 : 
A1 A3 A1 A4 A1 A4 A5
10:  11:
11:  12:
12: 
A1 A4 A5 A6 A1 A4 A5 A7 A1 A4 A5 A8
13:  14:
14:  9 :
9 : 
A1 A4 A5 A9 A1 A4 A5 A1 A4 A5
If the left cup is closer to the ground then that means the right cup is too
light; so we leave the last paper weight in that cup. If the right cup is closer
to the ground then that means the cup is too heavy; so we take the last paper
weight out and put it on the table again. If the balance is in equilibrium then
we usually decide to stop. Photograph (9) is repeated for comparison
with photograph (14): both show the balance "in equilibrium".
Here is a schematic overview of weighting the tomato and some other experiments:
pi| on table |right cup | |Half Banana| |Metal Strip| ct|AAAAAAAAAA|AAAAA AAAAA| |AAAAA AAAAA| |AAAAA AAAAA| nr|0123456789|01234 56789| |01234 56789| |01234 56789| --|----------------------| |-----------| |-----------| 3|XXXXXXXXXX| | |X | |X | 4| XXXXXXXXX|X | |XX | |XX | 5|X XXXXXXXX| X | |X X | |X X | 6|X XXXXXXX| XX | |X X | |X XX | 7|X X XXXXXX| X X | |X X |>< |X X X | 8|X XX XXXXX| X X | |X X X | |X X X | 9|X XX XXXX| X X X |>< |X X X | |X X XX | 10|X XX XXX| X X XX | |X X X | |X X XXX |>< 11|X XX X XX| X X X X | |X X X |>< |X X XXXX |>< 12|X XX XX X| X X X X |>< |X X X|>< |X X XXX X|>< 13|X XX XXX | X X X X|>< 10001.00000 10100.11100 14|X XX XXXX| X X X |>< Equilibrium Equilibrium 9|X XX XXXX| X X X |>< 10001.00010 10100.11110 Binary number 01001.10000 10001.00001 10100.11101
| weight A0 | |Zero Weight| |Heavy Metal|
|AAAAA AAAAA| |AAAAA AAAAA| |AAAAA AAAAA|
|01234 56789| |01234 56789| |01234 56789|
|-----------| |-----------| |-----------|
| | |X | |X |
| X | | X | |XX |
| XX | | X | |XXX |
| XXX | | X | |XXXX |
| XXXX | | X | |XXXXX |
| XXXX X | | X | |XXXXX X |
| XXXX XX | | X | |XXXXX XX |
| XXXX XXX | | X | |XXXXX XXX |
| XXXX XXXX |>< | X |>< |XXXXX XXXX |
| XXXX XXXXX|>< | X|>< |XXXXX XXXXX|
01111.11111 00000.00010 11111.11111
Theoretical 00000.00001 out of scope
10000.00000 Theoretical no equilibrium
00000.00000