Linear Tetrahedron
$
\newcommand{\dq}[2]{\displaystyle \frac{\partial #1}{\partial #2}}
\newcommand{\oq}[2]{\partial #1 / \partial #2}
$
It is strongly advised to read about the 2-D case first, before proceeding to
the more difficult 3-D algebra. It's in the section about
Triangle Isoparametrics.
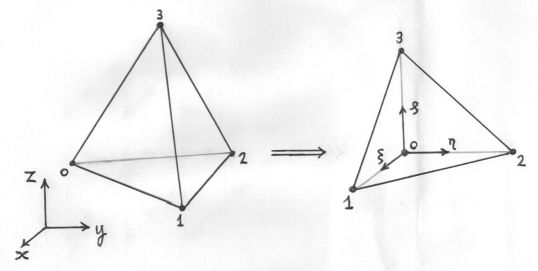
Let's consider the simplest non-trivial finite element shape in 3-D, which is
a linear tetrahedron. Function behaviour is approximated inside such a
tetrahedron by a linear interpolation between the function values at the
vertices, also called nodal points. Let $T$ be such a function, and $x,y,z$
coordinates, then:
$$
T = A.x + B.y + C.z + D
$$
Where the constants A, B, C, D are yet to be determined.
Substitute $ x=x_k $ , $ y=y_k $ , $ z=z_k $ with $ k=0,1,2,3 $.
Start with:
$$
T_0 = A.x_0 + B.y_0 + C.z_0 + D
$$
Clearly, the first of these equations can already be used to eliminate the
constant $D$, once and forever:
$$
T - T_0 = A.(x - x_0) + B.(y - y_0) + C.(z - z_0)
$$
Then the constants $A$ , $B$ , $C$ are determined by:
$$ \begin{array}{ll}
T_1 - T_0 = A.(x_1 - x_0) + B.(y_1 - y_0) + C.(z_1 - z_0) \\
T_2 - T_0 = A.(x_2 - x_0) + B.(y_2 - y_0) + C.(z_2 - z_0) \\
T_3 - T_0 = A.(x_3 - x_0) + B.(y_3 - y_0) + C.(z_3 - z_0)
\end{array} $$
Three equations with three unknowns. A solution can be found:
$$
\left[ \begin{array}{c} A \\ B \\ C \end{array} \right] =
\left[ \begin{array}{ccc} x_1-x_0 & y_1-y_0 & z_1-z_0 \\
x_2-x_0 & y_2-y_0 & z_2-z_0 \\
x_3-x_0 & y_3-y_0 & z_3-z_0 \end{array} \right]^{-1}
\left[ \begin{array}{c} T_1-T_0 \\ T_2-T_0 \\ T_3-T_0 \end{array} \right]
$$
It is concluded that $A,B,C$ and hence $(T-T_0)$ must be a linear expression
in the $(T_k-T_0)$:
$$
T - T_0 = \xi.(T_1 - T_0) + \eta.(T_2 - T_0) + \zeta.(T_3 - T_0)
$$ $$ =
\left[ \begin{array}{ccc} \xi & \eta & \zeta \end{array} \right]
\left[ \begin{array}{c} T_1-T_0 \\ T_2-T_0 \\ T_3-T_0 \end{array} \right]
$$
See above:
$$ =
\left[ \begin{array}{ccc} \xi & \eta & \zeta \end{array} \right]
\left[ \begin{array}{ccc} x_1-x_0 & y_1-y_0 & z_1-z_0 \\
x_2-x_0 & y_2-y_0 & z_2-z_0 \\
x_3-x_0 & y_3-y_0 & z_3-z_0 \end{array} \right]
\left[ \begin{array}{c} A \\ B \\ C \end{array} \right]
$$
See above:
$$ = T - T_0 =
\left[ \begin{array}{ccc} x-x_0 & y-y_0 & z-z_0 \end{array} \right]
\left[ \begin{array}{c} A \\ B \\ C \end{array} \right]
$$
Hence:
$$ \begin{array}{ll}
x - x_0 = \xi .(x_1 - x_0) + \eta.(x_2 - x_0) + \zeta.(x_3 - x_0) \\
y - y_0 = \xi .(y_1 - y_0) + \eta.(y_2 - y_0) + \zeta.(y_3 - y_0) \\
z - z_0 = \xi .(z_1 - z_0) + \eta.(z_2 - z_0) + \zeta.(z_3 - z_0)
\end{array} $$
But also:
$$
T - T_0 = \xi.(T_1 - T_0) + \eta.(T_2 - T_0) + \zeta.(T_3 - T_0)
$$
Therefore the same expression holds for the function $T$ as well as for
the coordinates $x,y,z$. This is called an isoparametric transformation.
It is remarked without proof that the local coordinates $\xi,\eta,\zeta$
within a tetrahedron can be interpreted as sub-volumes, spanned by the vectors
$ \vec{r}_k-\vec{r}_0 $ and $\vec{r}-\vec{r}_0 $ where $\vec{r}=(x,y,z) $ and
$k=1,2,3$.
Reconsider the expression:
$$
T - T_0 = \xi.(T_1 - T_0) + \eta.(T_2 - T_0) + \zeta.(T_3 - T_0)
$$
Partial differentiation to $ \xi $ , $ \eta $ , $ \zeta $ gives:
$$
\oq{T}{\xi} = T_1 - T_0 \quad ; \quad \oq{T}{\eta} = T_2 - T_0
\quad ; \quad \oq{T}{\zeta} = T_3 - T_0
$$
Therefore:
$$
T = T(0) + \xi \dq{T}{\xi} + \eta \dq{T}{\eta} + \zeta \dq{T}{\zeta}
$$
This is part of a Taylor series expansion around node (0). Such Taylor series
expansions are very common in Finite Difference analysis.
Now rewrite as follows:
$$
T = (1 - \xi - \eta - \zeta).T_0 + \xi.T_1 + \eta.T_2 + \zeta.T_3
$$
Here the functions $ (1-\xi-\eta-\zeta),\xi,\eta,\zeta $ are called the {\em
shape functions} of a Finite Element. Shape functions $N_k$ have the property
that they are unity in one of the nodes (k), and zero in all other nodes.
In our case:
$$
N_0 = 1-\xi-\eta-\zeta \quad ; \quad N_1 = \xi \quad ; \quad N_2 = \eta
\quad ; \quad N_3 = \zeta
$$
So we have two representations, which are allmost trivially equivalent:
$$ \begin{array}{ll}
T = T_0 + \xi.(T_1 - T_0) + \eta.(T_2 - T_0) + \zeta.(T_3 - T_0) \quad
& \mbox{: Finite Difference} \\
T = (1 - \xi - \eta - \zeta).T_0 + \xi.T_1 + \eta.T_2 + \zeta.T_3 \quad
& \mbox{: Finite Element}
\end{array} $$
%
What kind of terms can be discretized at the domain of a linear tetrahedron?
In the first place, the function $T(x,y,z)$ itself, of course. But one may also
try on the first order partial derivatives $\oq{T}{(x,y,z)}$. We find:
$$
\oq{T}{x} = A \quad ; \quad \oq{T}{y} = B \quad ; \quad \oq{T}{z} = C
$$
Using the expressions which were found for $A,B,C$:
$$
\left[ \begin{array}{c} \oq{T}{x} \\ \oq{T}{y} \\ \oq{T}{z} \end{array}\right]
=\left[ \begin{array}{ccc} x_1-x_0 & y_1-y_0 & z_1-z_0 \\
x_2-x_0 & y_2-y_0 & z_2-z_0 \\
x_3-x_0 & y_3-y_0 & z_3-z_0 \end{array}\right]^{-1}
\left[ \begin{array}{c} T_1-T_0 \\ T_2-T_0 \\ T_3-T_0 \end{array}\right]
$$
It is seen from this formula that one must determine the inverse of the above
matrix first. Then add up the rows of the inverted matrix and provide the sum
with a minus sign, in order to find the coefficients belonging to $T_0$.
The result is a $3 \times 4$ Differentiation Matrix, which represents
the gradient operator $\oq{}{(x,y,z)}$ for the function values $T_{0,1,2,3}$
at a linear tetrahedron. Define:
$$
\begin{bmatrix} d_{11} & d_{12} & d_{13} \\
d_{21} & d_{22} & d_{23} \\
d_{31} & d_{32} & d_{33} \end{bmatrix} =
\begin{bmatrix} x_1-x_0 & y_1-y_0 & z_1-z_0 \\
x_2-x_0 & y_2-y_0 & z_2-z_0 \\
x_3-x_0 & y_3-y_0 & z_3-z_0 \end{bmatrix}^{-1}
$$
It follows that:
$$
\begin{bmatrix} \partial T / \partial x \\ \partial T / \partial y \\ \partial T / \partial z \end{bmatrix}
= \begin{bmatrix} d_{11} & d_{12} & d_{13} \\
d_{21} & d_{22} & d_{23} \\
d_{31} & d_{32} & d_{33} \end{bmatrix}
\begin{bmatrix} T_1 \\ T_2 \\ T_3 \end{bmatrix} -
\begin{bmatrix} d_{11} & d_{12} & d_{13} \\
d_{21} & d_{22} & d_{23} \\
d_{31} & d_{32} & d_{33} \end{bmatrix}
\begin{bmatrix} T_0 \\ T_0 \\ T_0 \end{bmatrix} \\
= \begin{bmatrix} d_{11} & d_{12} & d_{13} \\
d_{21} & d_{22} & d_{23} \\
d_{31} & d_{32} & d_{33} \end{bmatrix}
\begin{bmatrix} T_1 \\ T_2 \\ T_3 \end{bmatrix} -
T_0 \begin{bmatrix} d_{11} + d_{12} + d_{13} \\
d_{21} + d_{22} + d_{23} \\
d_{31} + d_{32} + d_{33} \end{bmatrix} \\
= \begin{bmatrix} - (d_{11} + d_{12} + d_{13}) & d_{11} & d_{12} & d_{13} \\
- (d_{21} + d_{22} + d_{23}) & d_{21} & d_{22} & d_{23} \\
- (d_{31} + d_{32} + d_{33}) & d_{31} & d_{32} & d_{33} \end{bmatrix}
\begin{bmatrix} T_0 \\ T_1 \\ T_2 \\ T_3 \end{bmatrix}
$$
So the $3 \times 4$ differentiation matrix is:
$$
\begin{bmatrix} \partial / \partial x \\ \partial / \partial y \\ \partial / \partial z \end{bmatrix}
= \begin{bmatrix} - (d_{11} + d_{12} + d_{13}) & d_{11} & d_{12} & d_{13} \\
- (d_{21} + d_{22} + d_{23}) & d_{21} & d_{22} & d_{23} \\
- (d_{31} + d_{32} + d_{33}) & d_{31} & d_{32} & d_{33} \end{bmatrix}
$$
