Polygons of low order
$
\def \hieruit {\quad \Longrightarrow \quad}
\def \slechts {\quad \Longleftrightarrow \quad}
\def \half {\frac{1}{2}}
\def \MET {\qquad \mbox{where} \quad}
\def \VOOR {\qquad \mbox{for} \quad}
\def \EN {\quad \mbox{and} \quad}
$
Without loss of generality, with a regular polygon, one vertex may be located at $(1,0)$. And since all vertices are the same,
attention may be restricted to that vertex. If only the polygon itself is considered, our fuzzyness equation is simplified
a great deal herewith:
$$
C(1,0,\sigma) = \sum_{k=0}^{N-1} e^{-\half \left\{\left[1-\cos(t_k)\right]^2 + \left[0-\sin(t_k)\right]^2\right\}/\sigma^2}\Delta t
\\ \MET \Delta t = 2\pi/N \quad ; \quad t_k = k.\Delta t \hieruit \\
C(1,0,\sigma) = \frac{2\pi}{N}\sum_{k=0}^{N-1} e^{-\half \left\{2-2\cos(k.2\pi/N)\right\}/\sigma^2}
$$
The exponent can be rewritten as:
$$
2-2\cos(k.2\pi/N) = 2-2\left[1-2\sin^2(k.\pi/N)\right]=\left[2\sin(k.\pi/N)\right]^2 \hieruit \\
C(1,0,\sigma) = \frac{2\pi}{N}\sum_{k=0}^{N-1} e^{-\half\left[2\sin(k.\pi/N)/\sigma\right]^2}
$$
The square of a (normed) side is recognized for $k=1$.
Let's switch now to some details.
It may happen that $1-\alpha.\sigma$ is negative; then the midpoint of the (unit) circle starts to fill in with non-zero values.
This is the case for polygons with a less or equal number of edges than a Dodecagon:
$$
\alpha.\sigma > 1 \slechts \alpha\frac{\sin(\pi/N)}{\pi}\alpha > 1 \slechts \sin(\pi/N) > \frac{\pi}{\alpha^2}
\\ \slechts N < \frac{\pi}{\arcsin\left(\pi/\alpha^2\right)} = 12.3 \approx \alpha^2 = 12.5
$$
Only a small part of the vertices at the circumscribed circle is taken into account for small angles / many sides.
This starts to change with the hexagon:
$$
\alpha.\sigma > 2 \slechts N < \frac{\pi}{\arcsin\left(\pi/\alpha^2/2\right)} = 6.0 \approx \alpha^2/2 = 6.2
$$
Another interesting question to ask is at which discretization the inner area
of the circle becomes so much crowded with black pixels that the curve itself
cannot be observed anymore. Four cases are distinguished.
At the angle increment $\pi/3$ , our fuzzyfied circle is in fact a hexagon.
For each of the vertices of that hexagon, we calculate
the contributions from itself and the other vertices, as compared with the
contributions to the midpoint:
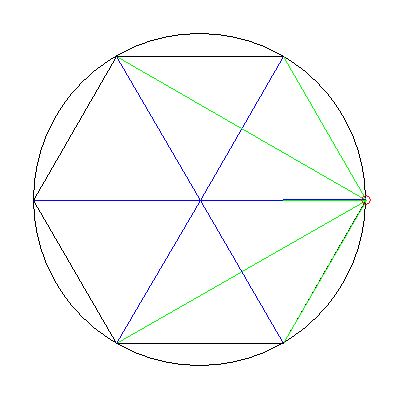
And let us in view of the above assume that these contributions cancel out each other,
ipse est (vertex = center):
$$
\frac{N}{2\pi} C(1,0,\sigma) =
e^{-0/(2\sigma^2)} + 2\,e^{-1/(2\sigma^2)} + 2\,e^{-(\sqrt{3})^2/(2\sigma^2)}
+ e^{-2^2/(2\sigma^2)} = 6\,e^{-1/(2\sigma^2)} \\
e^{-1/(2\sigma^2)} = x \hieruit \begin{cases}
1 + 2x + 2x^3 + x^4 = 6x \slechts x^4 + 2x^3 - 4x + 1 = 0 \\
-1/(2\sigma^2) = \ln(x) \slechts \sigma = 1/\sqrt{2\ln(1/x)} \end{cases}
$$
With $N=6$, it follows that:
$$
\sigma = \frac{\sin(\pi/N)}{\pi}\alpha \EN \alpha = \sqrt{2\ln(2/\epsilon)}
\\ \hieruit \alpha = \frac{\pi.\sigma}{\sin(\pi/N)} \EN \epsilon = 2\,e^{-\half\alpha^2}
$$
It's easy to see that one solution of $x^4 + 2x^3 - 4x + 1 = 0$ is given by $x=1$.
The meaning of this is an infinitely large spread $\sigma$, blurring the whole universe:
$$
e^{-1/(2\sigma^2)} = 1 \slechts 1/(2\sigma^2) = 0 \slechts \sigma = \infty
$$
corresponding in turn with a tolerance $\epsilon = 0$.
The equation as a whole, after
dividing it by $(x-1)$, could have been solved by hand, but I am lazy. With MAPLE:
solve(x^4 + 2*x^3 - 4*x + 1 = 0,x);
Giving as real valued solutions, indeed $x=1$ and $x=2^{1/3}-1$. Numerical values are:
N = 6
x = 0.25992
sigma = 0.60917 <> 0.56217
alpha = 3.82754 <> 3.53223
eps = 0.00132 <> 0.00391
vertex - center = 0.19697
Results with our standard tolerance $\epsilon=1/256$ are given on the right for comparison.
It is seen that, with the standard values for $\sigma$, $\alpha$ and $\epsilon$, the darkness at the center is somewhat less
than the darkness at a polygon vertex; meaning that the accompanying circle still can be vaguely distinguished from its background.
The break-even error is smaller than our 256 shades of gray error and the corresponding values of $\alpha$ and $\sigma$ are larger.
At first the following question shall be answered:
How to prove $\cos\left(\frac{2\pi}{5}\right)=\frac{\sqrt{5}-1}{4}$?
Then we have for the exponent $2-2\cos(2\pi/5)$:
$$
2-2\cos(2\pi/5) = 2-2\frac{\sqrt{5}-1}{4} = \frac{5-\sqrt{5}}{2}
$$
This is correct; the length of one side of the pentagon with circumscribed unit circle is known to be:
$$
\sqrt{\left[2\sin(1.\pi/5)\right]^2} = \sqrt{\frac{5-\sqrt{5}}{2}}
$$
For $2-2\cos(2.2\pi/5)$ we have:
$$
\cos(2.2\pi/5) = 2\cos^2(2\pi/5)-1 = \frac{-1-\sqrt{5}}{4} \hieruit \\ 2-2\cos(2.2\pi/5) = \frac{5+\sqrt{5}}{2}
$$
Hence for the pentagon the following break-even equation is found:
$$
e^{-1/(2\sigma^2)} = x \hieruit 1 + 2 x^{(5-\sqrt{5})/2} + 2 x^{(5+\sqrt{5})/2} - 5 x = 0
$$
We have given up any attempt to solve such an equation analytically and did it numerically, with MAPLE.
Don't forget to divide by the trivial outcome $x=1$ first:
fsolve((1+2*x^(5/2-sqrt(5)/2)+2*x^(5/2+sqrt(5)/2)-5*x)/(x-1)=0,x);
0.2683875064
The formulas for $\sigma$, $\alpha$ and $\epsilon$ as found with the hexagon remain valid for the pentagon, with $N=5$:
$$
\sigma = 1/\sqrt{2\ln(1/x)} \EN \alpha = \frac{\pi.\sigma}{\sin(\pi/N)} \EN \epsilon = 2\,e^{-\half\alpha^2}
$$
Numerical values are, on the left with these formulas and on the right with the standard $\epsilon = 1/256$:
N = 5
x = 0.26839
sigma = 0.61655 <> 0.66087
alpha = 3.29534 <> 3.53223
eps = 0.00877 <> 0.00391
vertex - center = -0.14855
It is seen that, with the standard values for $\sigma$, $\alpha$ and $\epsilon$, the darkness at the center is somewhat greater
than the darkness at a polygon vertex; meaning that the accompanying circle can no longer can be distinguished clearly.
The break-even error is larger than our 256 shades of gray error and the corresponding values of $\alpha$ and $\sigma$ are smaller.
The break-even equation in this case is the vertex itself plus two sides with length $\sqrt{2}$ plus two times the radius
equals four contributions with radius $1$:
$$
e^{-0/(2\sigma^2)} + 2\,e^{-(\sqrt{2})^2/(2\sigma^2)} + e^{-2^2/(2\sigma^2)} = 4\,e^{-1/(2\sigma^2)} \\
e^{-1/(2\sigma^2)} = x \hieruit 1 + 2x^2 + x^4 = 4x \slechts x^4+2x^2-4x+1 = 0
$$
A fourth order algebraic equation, too difficult to solve by hand:
solve(x^4+2*x^2-4*x+1,x);
Giving, apart from the trivial $x=1$ solution and ignoring complex solutions:
$$
x = \frac{(26+6\sqrt{33})^{1/3}}{3}-\frac{8}{3(26+6\sqrt{33})^{1/3}}-\frac{1}{3}
$$
With the same formulas for $\sigma$, $\alpha$ and $\epsilon$, numerical values are:
N = 4
x = 0.29560
sigma = 0.64051 <> 0.79503
alpha = 2.84572 <> 3.53223
eps = 0.03488 <> 0.00391
vertex - center = -0.36014
The column on the right shows that the distinction between polygon and background has become even more blurred.
The break-even error is much larger than our 256 shades of gray error and the corresponding values of $\alpha$
and $\sigma$ are smaller, but not so much.
Still another special case is the equilateral triangle. Analogously we then have:
$$
e^{-0/(2\sigma^2)} + 2\,e^{-(\sqrt{3})^2/(2\sigma^2)} = 3\,e^{-1/(2\sigma^2)} \\
e^{-1/(2\sigma^2)} = x \hieruit 1 + 2x^3 = 3x \slechts 2x^3 - 3x + 1 = 0
$$
It's easy to see, again, that one solution of this equation is given by $x=1$ and:
$$
\frac{2x^3 - 3x + 1}{x-1} = 2x^2+2x-1 = 0 \hieruit x = \half\left(\sqrt{3}-1\right)
$$
With the same formulas for $\sigma$, $\alpha$ and $\epsilon$, numerical values are:
N = 3
x = 0.36603
sigma = 0.70533 <> 0.97371
alpha = 2.55864 <> 3.53223
eps = 0.07576 <> 0.00391
vertex - center = -0.35939
Animation


