Shannon's Sampling Theorem
$
\def \hieruit {\quad \Longrightarrow \quad}
\def \slechts {\quad \Longleftrightarrow \quad}
\def \sinc {\operatorname{sinc}}
$
We are going to consider a uniform comb of sinc functions. The width $\,\sigma\,$
of such a sinc function is defined, rather arbitrary, as the place most close
to $\,x=0\,$ where it is zero:
$$
\sinc(q\,\sigma) = 0 \hieruit q\,\sigma = \pi \hieruit q = \frac{\pi}{\sigma}
$$
And this function must be normed:
$$
\int_{-\infty}^{+\infty} \sinc\left(\frac{\pi}{\sigma} x\right) \, dx
= \frac{\sigma}{\pi}
\int_{-\infty}^{+\infty} \sinc\left(\frac{\pi}{\sigma} x\right)
\, d\left(\frac{\pi}{\sigma} x \right) = \frac{\sigma}{\pi} \pi = \sigma
$$
So the normed sinc function with spread $\,\sigma\,$ is:
$$
\frac{1}{\sigma} \sinc\left(\frac{\pi}{\sigma} x\right)
$$
In order to be able to proceed, the Fourier integral of it shall be calculated:
$$
\frac{1}{\sigma}
\int_{-\infty}^{+\infty} \sinc\left(\frac{\pi}{\sigma} x\right) \cos(y x)\, dx
= \frac{1}{\sigma} \frac{\sigma}{\pi} \int_{-\infty}^{+\infty} \sinc(\xi)
\cos\left(\left[\frac{\sigma}{\pi}y\right] \xi\right) \, d\xi
$$
Where we have put $\,\pi x/\sigma = \xi\,$. The latter outcome is equal to a block
function $\,B_\sigma (y)\,$, where:
$$
B_\sigma (y) = \left\{ \begin{array}{lll}
0 & \mbox{for} & \sigma/\pi y < -1 \\
\pi/\pi & \mbox{for} & -1 < \sigma/\pi y < +1 \\
0 & \mbox{for} & +1 < \sigma/\pi y
\end{array} \right.
$$
Written otherwise:
$$
B_\sigma (y) = \left\{ \begin{array}{lll}
0 & \mbox{for} & y < -\pi/\sigma \\
1 & \mbox{for} & -\pi/\sigma < y < +\pi/\sigma \\
0 & \mbox{for} & +\pi/\sigma < y
\end{array} \right.
$$
Conclusion - remember that $\,\omega = 2\pi/\Delta\,$:
$$
\sum_{L=-\infty}^{+\infty} \frac{\Delta}{\sigma}
\sinc\left(\frac{\pi}{\sigma}\left[ x - L \Delta \right]\right) =
1 + 2 \times \sum_{k=1}^\infty B_\sigma(k\omega) \cos(k\omega x)
$$
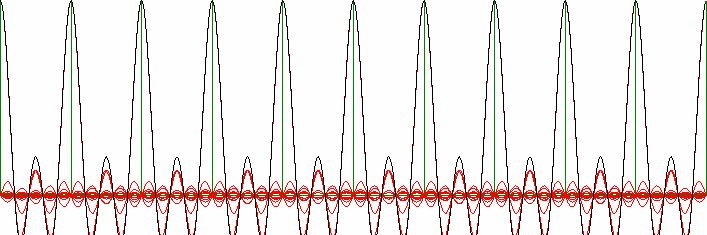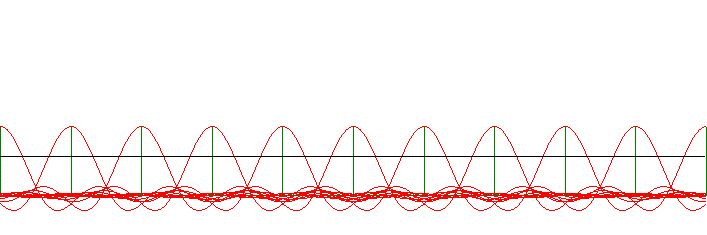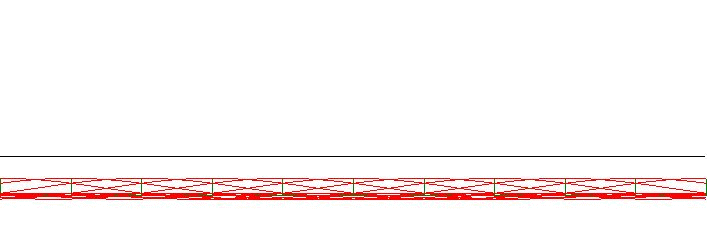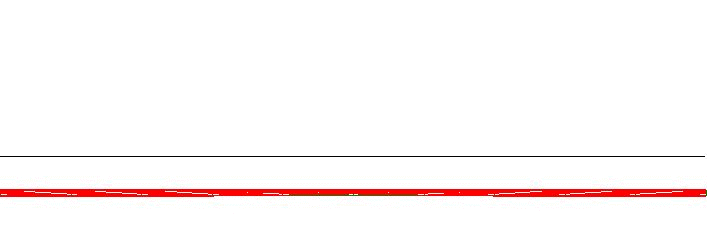
The right hand side is exactly equal to one iff for all $\,k > 1\,$:
$$
+\pi/\sigma < k\omega \slechts \pi \frac{\Delta}{2\pi} < \sigma \slechts
\sigma > \frac{\Delta}{2}
$$
A true miracle has happened. There is no error present, at all, in the
following formula. Which thus holds exactly, for any $\,\sigma > \Delta/2\,$:
$$
\sum_{k=-\infty}^{+\infty} \frac{\Delta}{\sigma}
\sinc\left(\frac{\pi}{\sigma}\left[ x - k \Delta \right]\right) = 1
$$
Where have we seen this before .. ? Let $\,f(x) = 1$ and $f_k = f(k\Delta)\,$ and
do a trivial rewrite:
$$
\sum_{k=-\infty}^{+\infty} \frac{\Delta}{\sigma}\, f_k \,
\sinc\left(\frac{\pi}{\sigma}\left[ x - k \Delta \right]\right) = f(x)
$$
Now take a look at
Shannon's Sampling Theorem.
It should be obvious that there exists a correspondence with our own theory.
It is also clear that the Special Theory of Continuity can, in principle,
be modified as to include general function behaviour as well: $\,f(x) \neq 1\,$.
And there is a section Nonuniform sampling in that web page, where we can
read about a second item on our To Do list: the sampling theory of Shannon can
be generalized for the case of nonuniform samples.
