Approximate Density
$
\def \half {\frac{1}{2}}
\def \hieruit {\quad \Longrightarrow \quad}
\def \slechts {\quad \Longleftrightarrow \quad}
\def \OF {\quad \mbox{or} \quad}
\def \MET {\quad \mbox{with} \quad}
$
The reverse question. Suppose that the sense $P(x)$ is given,
how can we find then the associated density of points $\{x_k\}$ ?
A crude approximation is to
take the value $P(x_k)$ at the position $x_k$ and construct the next point by
demanding that the rectangle with height $P(x_k)$ and width $(x_{k+1}-x_k)$
has an area equal to one:
$$
P(x_k) (x_{k+1}-x_k) = 1 \hieruit
x_{k+1} = x_k + \frac{1}{P(x_k)}
$$
Herewith it is assumed that $P(x)$ is positive everywhere. But, as we have seen
with the guitar example in the previous section, it is also possible that $P(x)$
is negative everywhere, giving rise to a monotone decreasing sequence.
In that case, the x-axis shall be traversed in the opposite direction, giving:
$$
P(x_k) (x_k-x_{k-1}) = 1 \hieruit
x_{k-1} = x_k - \frac{1}{P(x_k)}
$$
Anyway, a much better job can be done as follows. Consider a linear approximation
of the sense in the neighbourhood of $x_k$:
$$
P_{k+1} = P(x_k) + P'(x_k) (x_{k+1} - x_k)
$$
Where it is noticed that the estimate $P_{k+1}$ may be almost, but not exactly
equal to $P(x_{k+1})$.
The density may be approximated with help of the trapezium rule as well:
$$
\half \left[ P_{k+1} + P(x_k) \right] \left[x_{k+1} - x_k\right] = 1
$$
Substitution of the first formula into the second gives:
$$
\half \left[ P(x_k) + P'(x_k) (x_{k+1} - x_k) + P(x_k) \right]
\left[x_{k+1} - x_k\right] = 1
$$ $$
\hieruit
\left[ \half P'(x_k) \right] (x_{k+1} - x_k)^2 + P(x_k)(x_{k+1} - x_k) - 1 = 0
$$
A quadratic equation. Solve for $(x_{k+1} - x_k)$ :
$$
x_{k+1} - x_k = \frac{ - P(x_k) \pm \sqrt{P^2(x_k) + 2 P'(x_k)}}{P'(x_k)}
$$
Take as an example the linear density:
$$
P(x) = \frac{1}{\Delta^2}\left(x+\frac{\Delta}{2}\right) \hieruit P'(x)= \frac{1}{\Delta^2}
\hieruit \\ x_{k+1} - x_k =
\frac{ - (x_k+\Delta/2)/\Delta^2 \pm \sqrt{\left[(x_k+\Delta/2)/\Delta^2\right]^2+ 2/\Delta^2}}{1/\Delta^2}
\hieruit \\ x_{k+1} = \pm \sqrt{(x_k+\Delta/2)^2 + 2\Delta^2}-\Delta/2
$$
Compare with a previously found result to establish that the sign of $\pm$ must be plus:
$$
x_k = \left( \sqrt{1/4 + 2 k}-1/2 \right) \Delta \hieruit (x_k+\Delta/2)^2 = \Delta^2(1/4 + 2 k)^2 \hieruit \\
x_{k+1} = \pm \Delta\sqrt{(1/4 + 2 k) + 2}-\Delta/2 = \left( \sqrt{1/4 + 2 (k+1)}-1/2 \right) \Delta
$$
It should be no surprise that the outcome for a linear density is
not approximate but exact.
Anyway, quite in general, we still have:
$$
x_{k+1} - x_k = \frac{\sqrt{P^2(x_k) + 2 P'(x_k)} - P(x_k)}{P'(x_k)}
$$
The numerator is of the form $(a-b)$. Now multiply with $(a+b)/(a+b)$,
leading to values of $(a^2-b^2)/(a+b)$ which are likely more stable numerically:
$$
x_{k+1} - x_k = \frac{2 P'(x_k)/P'(x_k)}{\sqrt{P^2(x_k) + 2 P'(x_k)} + P(x_k)} \\
\hieruit x_{k+1} = x_k +
\frac{1}{\sqrt{\left[P(x_k)/2\right]^2 + P'(x_k)/2} + P(x_k)/2}
$$
The plus sign (out of $\pm\sqrt{}$) also comes from the fact that, for $P'(x) = 0$,
the next point has to be found by the (no longer) crude approximation: $x_{k+1} =
x_k + 1/P(x_k)$. It is noticed, in addition, that the expression under the
square root should not become negative. Meaning that, if $P'(x_k) < 0$:
$$
| P'(x_k) | < \half \left[ P(x_k) \right]^2
$$
It can be argued, though, that the above condition must also hold for positive
values of $P'(x_k)$. The reason is that the sequence $x_k$ could be traversed in
the opposite direction as well:
$$
\left. \begin{array}{l}
f_{k-1} = P(x_k) + P'(x_k) (x_{k-1} - x_k) \\
\half \left[ P(x_k) + f_{k-1} \right] \left[x_{k-1} - x_k\right] = -1
\end{array} \right\} \hieruit
$$ $$
\left[ \half P'(x_k) \right] (x_{k-1} - x_k)^2 + P(x_k)(x_{k-1} - x_k) + 1 = 0
$$ $$
\left[ \half P'(x_k) \right] (x_{k+1} - x_k)^2 + P(x_k)(x_{k+1} - x_k) - 1 = 0
$$
Thus $(k+1)$ changes into $(k-1)$ means that $+1$ changes into $-1$. And that's
the only difference between traversing in a positive or in a negative direction.
A bit of further thinking reveals then that the negative end-result must be:
$$
x_{k-1} = x_k +
\frac{1}{\sqrt{\left[P(x_k)/2\right]^2 - P'(x_k)/2} + P(x_k)/2}
$$
And therefore, again, the abovementioned condition must hold:
$$
| P'(x_k) | < \half \left[ P(x_k) \right]^2
$$
Take for example the linear density, where $P(x) = (x/\Delta + \half)/\Delta$,
$P'(x) = 1/\Delta^2$. Then our condition translates into:
$$
| P'(x_k) | < \half \left[ P(x_k) \right]^2 \slechts
1/\Delta^2 < \half \left[ (x_k/\Delta + \half)/\Delta \right]^2 \slechts
$$ $$
\left[ (x_k/\Delta + \half) \right]^2 > 2
\slechts x_k/\Delta > - \half + \sqrt{2} \OF x_k/\Delta < - \half - \sqrt{2}
$$
Only the non-negative solution must be kept. We conclude that the algoritm for
constructing the set $\{x_k\}$ from the linear sense
$P(x) = (x/\Delta + \half)/\Delta$ will certainly work for
$x_k > (\sqrt{2} - 1/2) \Delta \approx 0.9142135 \Delta$ , let's say $x_k > \Delta$,
which is certainly the case for $k > 0$.
Take as an example the sense that is an approximation for the longitudinal wave
with small amplitude, eventually without the latter restriction:
$$
P(x_k) = \frac{1}{\Delta}\left[1 - A\frac{2\pi}{\lambda}\cos\left(\frac{2\pi}{\lambda} x_k\right)\right]
\hieruit \\
P'(x_k) = \frac{A}{\Delta}\left(\frac{2\pi}{\lambda}\right)^2\sin\left(\frac{2\pi}{\lambda} x_k\right)
$$
From which the iteration scheme follows. The result is:
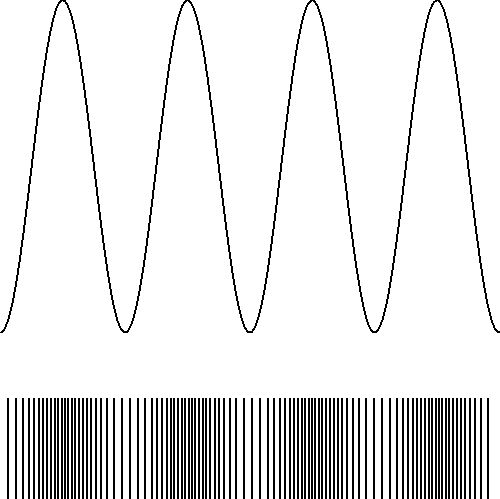
Accompanying software for making the pictures is
disclosed as well.

