Resistor networks
Main reference is Electric circuit diagram equivalents of fields
by Gerard Westendorp. Also of interest may be the Lumped-element model.
Crucial is the following. According to Kirchhoff's circuit laws
a basic property of resistor networks is that the net current to a nodal point / entering a junction $(i)$ is zero:
$$
\sum_j I_{ij} = 0 \quad \Longleftrightarrow \quad \sum_j (V_j-V_i)/R_{ij} = 0
$$
Working out for separate resistors $R$ , it can be seen that the equations are a finite Element assembly of symmetric
$2\times 2$ matrices:
$$
{\bf E} = \begin{bmatrix} +1/R & -1/R \\ -1/R & +1/R \end{bmatrix}
$$
Thus we have landed on solid ground, according to the
Definition of finite elements (Ciarlet).
Software has been developed for the purpose:
Examples
inlezen netS1 netS2
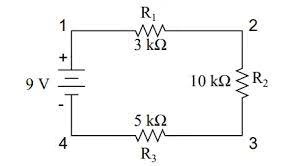
Bulk:
1 2 3.
2 3 10.
3 4 5.
Prescribed:
4 1 9.
Output:
# unknowns = 4
bandwidth = 2
Resistors:
1 2 3.00000
2 3 10.00000
3 4 5.00000
Prescribed:
4 1 9.00000
Voltages:
1 9.00000
2 7.50000
3 2.50000
4 0.00000
Amperages:
1 2 0.50000
2 3 0.50000
3 4 0.50000
1 4 0.50000
Resistance:
1 4 18.00000
Dissipation = 4.50000
inlezen netP1 netP2
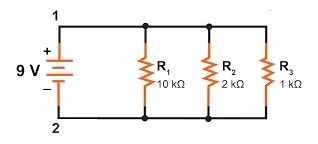
Bulk:
1 2 10.
1 2 2.
1 2 1.
Prescribed:
2 1 9.
Output:
# unknowns = 2
bandwidth = 2
Resistors:
1 2 10.00000
1 2 2.00000
1 2 1.00000
Prescribed:
2 1 9.00000
Voltages:
1 9.00000
2 0.00000
Amperages:
1 2 0.90000
1 2 4.50000
1 2 9.00000
1 2 14.40000
Resistance:
1 2 0.62500
Dissipation = 129.60000
inlezen netP1a netP2a
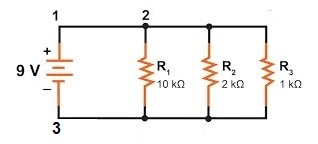
Bulk:
2 3 10.
2 3 2.
2 3 1.
1 2 0.
Prescribed:
3 1 9.
Output:
# unknowns = 3
bandwidth = 2
Resistors:
2 3 10.00000
2 3 2.00000
2 3 1.00000
1 2 0.00000
Prescribed:
3 1 9.00000
Voltages:
1 9.00000
2 9.00000
3 0.00000
Amperages:
2 3 0.90000
2 3 4.50000
2 3 9.00000
1 2 14.40000
1 3 14.40000
Resistance:
1 3 0.62500
Dissipation = 129.60000


