Propositional Logic and Redundancy

There are Philosophical problems with the Material conditional. The Dutch philosopher Emanuel Rutten has written an article about it, titled: Dissolving the Scandal of Propositional Logic? From that article we quote, as an example which is true in propositional logic but sounds illogical in common language, the following.

[2] Brigitte can mix green with yellow paint
    OR Brigitte can mix green with blue paint.

In the formalism of propositional logic it says: $(P \Rightarrow R) \vee (Q \Rightarrow R)$ with $R = P \wedge Q$. A truth table shows that this expression is a tautology. Now, from David Gries, "Compiler Construction for Digital Computers", John Wiley & Sons, 1971, we alternatively have: 

c OR d   is defined by  IF c THEN TRUE  ELSE  d
c AND d  is defined by  IF c THEN   d   ELSE FALSE
  NOT c  is defined by  IF c THEN FALSE ELSE TRUE
c ==> d  is defined by  IF c THEN   d   ELSE TRUE
c        is defined by  IF c THEN TRUE  ELSE FALSE
Thus, in a sequential sense - according to Gries - the tautology $(P \Rightarrow R) \vee (Q \Rightarrow R)$ reads as follows. 
if (if P then R else TRUE) then TRUE else (if Q then R else TRUE)
In most programming languages boolean expressions indeed seem to be subject to "lazy evaluation" of the above kind. Therefore we can replace the abovementioned sequential expression by its combinatorical equivalent again: $((\neg P) \vee R) \vee ((\neg Q) \vee R_{\_}(R))$. With a little adjustment for the second variable $R$: the function $R_{\_}(R)$ is identical to $R$ but it contains an alarm message in addition, namely: ' observed! '. A little program in Pascal shall make clearer what's going on here: 
program Rutten;

function r_(r : boolean) : boolean;
begin
  Write(' observed! ');
  r_ := r;
end;

procedure test;
var
  p,q,r : boolean;
  k : integer;
begin
  Writeln('P':6,'Q':6,'R':6,'(P=>R)v(Q=>R)':16);
  Writeln('-----------------------------------');
  for k := 0 to 3 do
  begin
    p := ((k div 2) = 0);
    q := ((k mod 2) = 0);
    r := (p and q);
    Writeln(p:6,q:6,r:6,((not p) or r) or ((not q) or r_(r)):12);
  { if (if p then r else true) then true else (if q then r else true) }
  end;
end;

begin
  test;
end.
Output (mind the absence of the alarm): 
     P     Q     R   (P=>R)v(Q=>R)
-----------------------------------
  TRUE  TRUE  TRUE        TRUE
  TRUE FALSE FALSE        TRUE
 FALSE  TRUE FALSE        TRUE
 FALSE FALSE FALSE        TRUE
The point is: the message ' observed! ' will never be observed!
The function $R_{\_}(R)$ is not executed in any way; it is like the program statement is simply not present. So what's left is this: $((\neg P) \vee R) \vee (\neg Q)$. In common language that is:

[2] Brigitte can mix green with yellow paint
    OR Brigitte has no blue paint.

Which sounds anyway more reasonable than the original statement.
It is also seen that the expression $(P \Rightarrow R) \vee (Q \Rightarrow R)$ is logically equivalent with this one: $((\neg P) \vee R) \vee ((\neg Q) \vee R) \equiv ((\neg P) \vee (\neg Q) \vee (R \vee R))$. The last instance of $R$ is obviously redundant.
Still anoher way of looking at our problem shall be presented. For ease of notation, let's replace TRUE by $1$ and FALSE by $0$ in $(P \Rightarrow R) \vee (Q \Rightarrow R)$ with $R = (P \wedge Q)$. Then, with the sequential interpretation and all possibilities covered: 

if (if P then R else 1) then 1 else (if Q then R else 1) : in general
if (if 0        else 1) then 1            [    ]         : P = 0
if (if 1 then 0       )        else (if 0 [    ] else 1) : P = 1, Q = 0
if (if 1 then 1       ) then 1            [    ]         : P = 1, Q = 1
So for the second instance of $R$ we have, with all possible (0,1) specifications, empty spots [ ]; the second instance of $R$ it is not decidable. It is like it is not there at all! The accompanying Flowchart is in concordance with this observation:

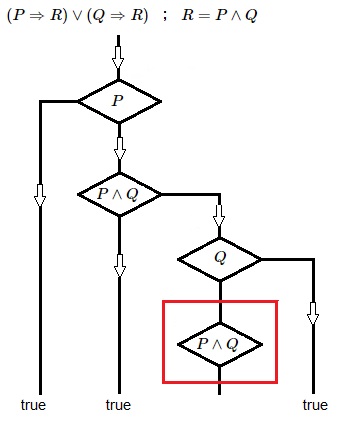
As a second example, consider the tautology $(P \Rightarrow Q) \vee (Q \Rightarrow P)$.
The sequential version is, with 0 = FALSE and 1 = TRUE and all possibilities exhausted: 
if (if P then Q else 1) then 1 else (if Q then P else 1) : in general
if (if 0        else 1) then 1            [    ]         : P = 0
if (if 1 then 0       )        else (if 0 [    ] else 1) : P = 1, Q = 0
if (if 1 then 1       ) then 1            [    ]         : P = 1, Q = 1
Empty spots [ ] again. So the second instance of P is obviously redundant. As is clear as well from the Flowchart:

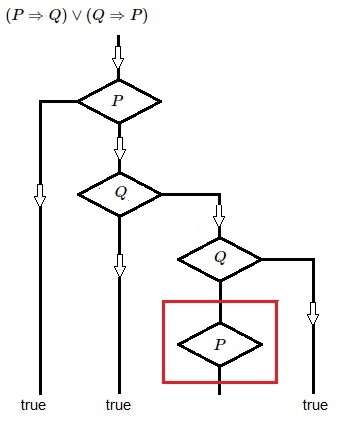
Not all propositional tautologies contain redundancies.
Time to present a counter example: $(P \Rightarrow Q) \Rightarrow (\neg Q \Rightarrow \neg P)$. 

if (if P then Q else 1) then (if -Q then -P else 1) else 1 : in general
if (if 0        else 1) then (if  1 then  1       )        : P = 0, Q = 0
if (if 0        else 1) then (if  0         else 1)        : P = 0, Q = 1
if (if 1 then 0       )                             else 1 : P = 1, Q = 0
if (if 1 then 1       ) then (if  0         else 1)        : P = 1, Q = 1
All instances of P and Q are decidable, none of these is redundant.
The tautology   IF(IF P THEN Q) THEN (IF NOT Q THEN NOT P)   is acceptable in common language as well. In the Flowchart all decisions are useful:

Question. When considering tautologies in Propositional Logic that sound "not good" in the logic of common language, does our notion of Redundancy, developed so far, provide a clue for dissolving that issue?
Unfortunately, the author has made a little mistake while trying to reproduce the problem from the article by Emanuel Rutten. What's actually in there is this: \begin{cases} \mbox{[1*] } P \wedge Q \Rightarrow R, \\ \mbox{[2*] } (P \Rightarrow R) \vee (Q \Rightarrow R). \end{cases} Here $P =$ “Brigitte has yellow paint”, $Q =$ “Brigitte has blue paint” and $R =$ “Brigitte can mix green”.
The calculus of propositional logic does render the argument form [1*]-[2*] logically valid.
The above may be concisely written as: $$ ((P \wedge Q) \Rightarrow R) \Rightarrow ((P \Rightarrow R) \vee (Q \Rightarrow R)) $$ Which is slightly different from what's stated in the question, where $\;R = (P \wedge Q)\;$ or $\;R \Leftrightarrow (P \wedge Q)\;$, where it should have been $\;R \Leftarrow (P \wedge Q)\;$.
With the sequential interpretation, as explained in the question, it reads, step by step: $$ \mbox{ if }(P \wedge Q \Rightarrow R) \mbox{ then } (P \Rightarrow R) \vee (Q \Rightarrow R) \mbox { else } 1\\ (P \wedge Q \Rightarrow R) \; \equiv \; (\mbox{ if } (\mbox{ if } P \mbox{ then } Q \mbox { else } 0) \mbox{ then } R \mbox { else } 1)\\ (P \Rightarrow R) \vee (Q \Rightarrow R) \; \equiv \; (\mbox{ if } (\mbox{ if } P \mbox{ then } R \mbox { else } 1) \mbox{ then } 1 \mbox { else } (\mbox{ if } Q \mbox{ then } R \mbox { else } 1)) $$ Flow chart and specification for all (0,1) values of (P,Q,R) are slightly more complicated than before.
But the end-result is the same: the last instance of R is redundant (: $\color{red}{\mbox{red box}}$ [ ] ). 

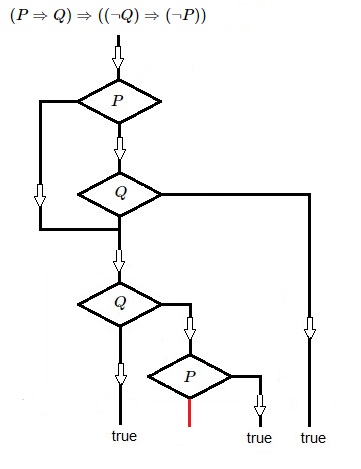
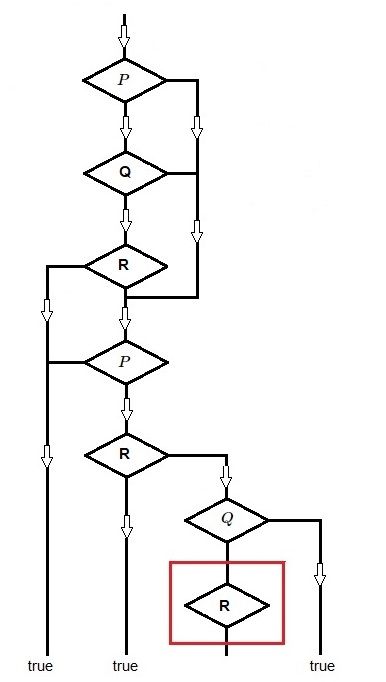
if (if (if P then Q else 0) then R else 1) then (if (if P then R else 1) then 1 else (if Q then R else 1)) else 1 : general
if (if (if 0        else 0)        else 1) then (if (if 0        else 1) then 1            [    ]                 : P = 0
if (if (if 1 then 0       )        else 1) then (if (if 1 then 0       )        else (if 0 [    ] else 1))        : P = 1 , Q = 0 , R = 0
if (if (if 1 then 0       )        else 1) then (if (if 1 then 1       ) then 1            [    ]                 : P = 1 , Q = 0 , R = 1
if (if (if 1 then 1       ) then 0                                                         [    ]          else 1 : P = 1 , Q = 1 , R = 0
if (if (if 1 then 1       ) then 1       ) then (if (if 1 then 1       ) then 1            [    ]                 : P = 1 , Q = 1 , R = 1
LATE EDIT. Further elaboration of Question & Answer in: