Calculate the surface area of each face of a hexahedron and it's outward normal, given coordinates
The problem is that, in general, the faces of an irregular hexahedron are not flat.
There is not one normal, the surface area is curved in space and difficult to
calculate exactly (whatever the additional value of "exact" is in a numerical context).
So I think you should anyway be satisfied with some sensible approximations. Here comes a proposal.
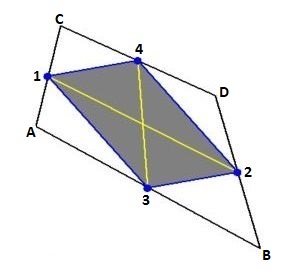
Let the vertices of the (in general non-planar) face of an irregular hexahedron be given
by $\,\vec{r}_A , \vec{r}_B , \vec{r}_C , \vec{r}_D$ ,
as shown in the picture. Then form the vertices of the gray (
Varignon) quadrilateral as :
$$\vec{r}_1 = \frac{1}{2}\left(\vec{r}_A+\vec{r}_C\right) \quad ; \quad
\vec{r}_2 = \frac{1}{2}\left(\vec{r}_B+\vec{r}_D\right) \\
\vec{r}_3 = \frac{1}{2}\left(\vec{r}_A+\vec{r}_B\right) \quad ; \quad
\vec{r}_4 = \frac{1}{2}\left(\vec{r}_C+\vec{r}_D\right)
$$
It can be easily proved that the quadrilateral $\overline{1324}$ is a paralellogram and hence
it is planar. The intersection point of the (yellow) diagonals of the Varignon paralellogram
is a good place to define the normal, as a vector perpendicular to $\overline{1324}$ . Last but not
least the total area of the face is defined by the sum of five planar areas: the area of the
paralellogram $\overline{1324}$ and the four areas of the triangles $\,\overline{A31} ,
\overline{B23} , \overline{D42} , \overline{C14}$ . Hope this helps.
