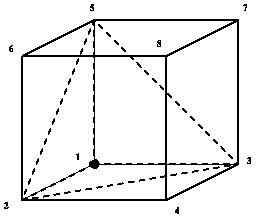

It is noticed that the tetrahedrons are not disjoint. Because I cannot look through the cube,
I have great difficulty imagining whether there is a hole left inside or not. If there is a hole,
what then is the shape of that hole? And what then is the volume of that hole?
The volume of one tetrahedron is $1/6$ . This would make a total of $\,8/6\,$ if they were disjoint,
but - as I've said - they are not. Apart from the facts some sort of proof would be nice.