Smooth Logarithm at zero/one with special conditions
Try a convolution with a function of small width and great height
(: Richard P. Feynman in Space-Time Approach to Quantum Electrodynamics ).
Name this function $\delta(x)$ (not quite by coincidence). The simplest one is this:
$$
\delta(x) = \begin{cases}
0 & \mbox{for} & x \le \epsilon \\
1/(2\epsilon) & \mbox{for} & -\epsilon \le x \le +\epsilon \\
0 & \mbox{for} & x \ge +\epsilon
\end{cases}
$$
The geometry of $\,\delta(x)\,$ is a rectangle with height $1/(2\epsilon)$ and width $2\epsilon$ ,
resulting in an area $1$, thus establishing that the function $\,\delta(x)\,$ is normed.
Now define:
$$ \overline{V}(x) =
\int_{-\infty}^{+\infty} \delta(x-t)\,V(t)\,dt
= \frac{1}{2\epsilon} \int_{x-\epsilon}^{x+\epsilon} V(t)\,dt
$$
With $\,\int \ln(t)\,dt = t\ln(t)-t$ . Then we have
for $\,x \le 1-\epsilon$ :
$$
\overline{V}(x) = \frac{1}{2\epsilon}\int_{x-\epsilon}^{x+\epsilon} 0 \,dt = 0
$$
for $\,1-\epsilon \le x \le 1+\epsilon$ :
$$
\overline{V}(x) =
\frac{1}{2\epsilon}\int_{x-\epsilon}^1 0 \,dt + \frac{1}{2\epsilon}\int_1^{x+\epsilon}\left[t\ln(t)-t\right]dt =
\left[(x+\epsilon)\ln(x+\epsilon)-(x+\epsilon)+1\right]/(2\epsilon)
$$
for $\,x \ge 1+\epsilon$ :
$$
\overline{V}(x) = \frac{1}{2\epsilon}\int_{x-\epsilon}^{x+\epsilon}\left[t\ln(t)-t\right]dt =
\left[(x+\epsilon)\ln(x+\epsilon)-(x-\epsilon)\ln(x-\epsilon)\right]/(2\epsilon)-1
$$
Sketch of the original $\,V(x)\,$ and its smoothed approximation $\,\color{red}{\overline{V}(x)}$ :
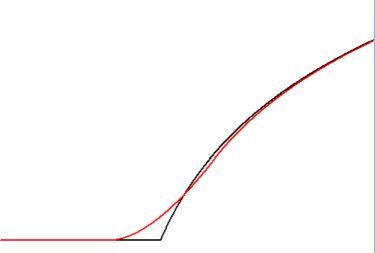
In this picture `eps` $\epsilon\,$ and viewport are defined as:
eps : double = 1;
xmin := -2; xmax := 5;
ymin := -0.1; ymax := 2.9;
