Quadrilateral Finite Elements must be convex and not self-intersecting. But why?
Main reference @ Mathematics Stack Exchange:
Quoted from this question:
> Why a quadrilateral with bilinear interpolation?
Little else is possible with polynomial terms like $\;1,\xi,\eta,\xi\eta\,$ , if
four nodal points are needed (one degree of freedom each) for obtaining four
equations with four unknowns. There still remain some issues, though, such as not self-intersecting and being convex.
That's precisely the content of this question. Exact answers, please; no hand waving as is common in some engineering contexts :-(
Related questions & answers @ Mathematics Stack Exchange, actually the studies preceding this answer:
Please take notice, because I'm not going to repeat everything that is already in these references.
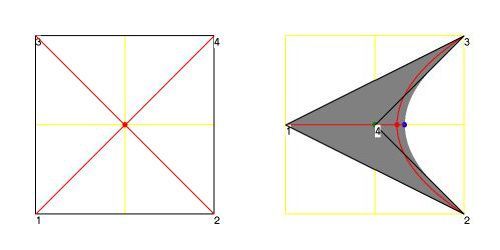
Then take a look at the picture below.
The shape in local coordinates $(\xi,\eta)$ , on the left, is a
$\left[-\frac{1}{2},+\frac{1}{2}\right] \times \left[-\frac{1}{2},+\frac{1}{2}\right]$
square. But the element in global coordinates $(x,y)$ can have a quite different shape,
like the one on the right:
The accompanying algebra - an isoparametric mapping with bi-linear interpolation - should be well known by now:
$$
\begin{cases}
x(\xi,\eta) = N_1 x_1 + N_2 x_2 + N_3 x_3 + N_4 x_4 \\
y(\xi,\eta) = N_1 y_1 + N_2 y_2 + N_3 y_3 + N_4 y_4
\end{cases}
$$
Where:
$$
\begin{cases}
N_1 = (\frac{1}{2}-\xi)(\frac{1}{2}-\eta)\\
N_2 = (\frac{1}{2}+\xi)(\frac{1}{2}-\eta)\\
N_3 = (\frac{1}{2}-\xi)(\frac{1}{2}+\eta)\\
N_4 = (\frac{1}{2}+\xi)(\frac{1}{2}+\eta)\\
\end{cases}
$$
The mapping of $\color{red}{\mbox{diagonals and midpoint}}$ has been displayed as well.
The meaning of the $\color{green}{\mbox{green}}$ dot at vertex $(4)$ and the rightmost
$\color{blue}{\mbox{blue}}$ dot will be explained soon.
It turns out that determining the inverse
transformation $\,\xi(x,y),\eta(x,y)$ , in general, is difficult, as has been
exemplified in an answer
by Nominal Animal.
Better a special case than no case at all.
So what we shall do is simplify the problem dramatically. First assume that we are only interested in function behaviour along
the diagonal $(1)-(4)$ , where $\,\xi=\eta$ . Then the isoparametric mapping simplifies to:
$$
\begin{cases}
x = (\frac{1}{2}-\xi)^2 x_1 + (\frac{1}{4}-\xi^2) (x_2 + x_3) + (\frac{1}{2}+\xi)^2 x_4 \\
y = (\frac{1}{2}-\xi)^2 y_1 + (\frac{1}{4}-\xi^2) (y_2 + y_3) + (\frac{1}{2}+\xi)^2 y_4 \end{cases}
$$
Now arrange the position of the vertices of the non-convex quadrilateral (see above picture) such that:
$$
\left[ \quad y_1 = 0 \quad \wedge \quad y_2=-y_3 \quad \wedge \quad y_4 = 0 \quad \right] \quad \Longrightarrow \quad y = 0
$$
Meaning that the problem is restricted at the $x$-axis only: it has become one-dimensional; it has become the study of a parabola $x(\xi)$ .
The same expression for $x$ can also be written as:
$$
x = \frac{1}{4}(x_1+x_2+x_3+x_4) + (x_4-x_1)\,\xi + (x_1-x_2-x_3+x_4)\,\xi^2\\
\mbox{or} \qquad x = a\,\xi^2+b\,\xi + c \quad \mbox{with} \; \begin{cases} a = x_1-x_2-x_3+x_4 \\ b = x_4-x_1 \\ c = (x_1+x_2+x_3+x_4)/4 \end{cases}
$$
The $\color{red}{\mbox{red spot}}$ is at $\,\xi=0$ . Hence : $x_{red} = (x_1+x_2+x_3+x_4)/4$ . Besides $y = 0$ , another red line
is the mapping of the diagonal $\xi = -\eta$ . It can be proved that this mapping is a parabola.
The $\color{blue}{\mbox{blue spot}}$ is at the maximum of the parabola $\,x = a\,\xi^2+b\,\xi + c$ . Assuming that $\,a<0$ , it's a matter of routine:
$$
x = a\left(\xi - \frac{b}{2a}\right)^2 + c - \frac{b^2}{4a} \quad \Longrightarrow \quad (\xi_{ blue},x_{ blue}) = \left(\frac{b}{2a},c - \frac{b^2}{4a}\right)
$$
The $\color{green}{\mbox{green spot}}$ is at one of the roots of the equation:
$$
(x_1-x_2-x_3+x_4)\,\xi^2 + (x_4-x_1)\,\xi + \frac{1}{4}(x_1+x_2+x_3+x_4) = x_4
$$
Because $x_4$ is a vertex, we know that the other root is always at $\,\xi = 1/2$ . Taking advantage of this fact we find:
$$
\left[\xi-\frac{1}{2}\right]\left[(x_1-x_2-x_3+x_4)\xi - \frac{1}{2}(x_1+x_2+x_3-3x_4)\right] = 0
$$
Time to introduce our final simplifications:
$$
(x_1,y_1) = (-\frac{1}{2},0) \quad ; \quad (x_2,y_2) = (+\frac{1}{2},-\frac{1}{2}) \quad ; \quad
(x_3,y_3) = (+\frac{1}{2},+\frac{1}{2}) \\ (x_4,y_4) = (H>0,0) = \mbox{variable}
$$
Then the $\color{green}{\mbox{green}}$ root of the equation for vertex (4) becomes:
$$
\left(-\frac{3}{2}+H\right)\xi - \frac{1}{2}\left(\frac{1}{2}-3H\right) = 0 \quad \Longrightarrow \quad \xi_{ green} = \frac{1-6H}{4H-6}
$$
It turns out that the denominator being zero corresponds with a parallelogram and a linear instead of quadratic interpolation.
Our current study doesn't cover that case.
Below is an animation of the shape of the quadrilateral, together with the parabola corresponding to the mapping $\,\xi \rightarrow x$ ,
for values of $H$ starting at $0$ with step size $1/8$ .
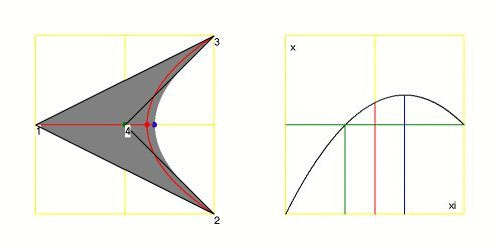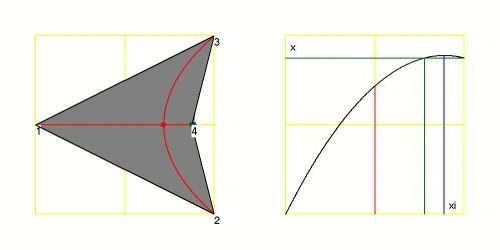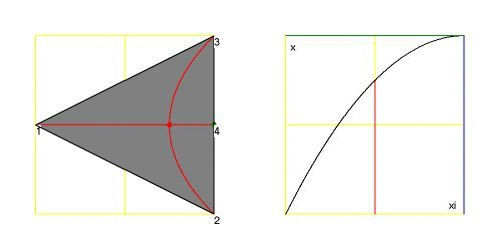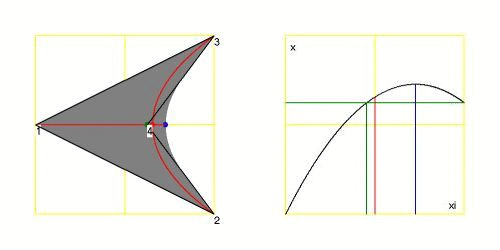
The $\color{green}{\mbox{green}}$ dot on the left corresponds with the $\color{green}{\mbox{green}}$ lines on the right: the position $(0,H)$ of vertex $(4)$.
It is seen that there are two values of $\xi$ with one value of $x$ for all $0 < H < 1/2$ , simply correponding with the two roots of our quadratic equation.
So the mapping at that vertex is not unique. The rightmost $\color{blue}{\mbox{blue}}$ dot on the left corresponds with the maximum of the parabola on the right.
It is trivial that this $\color{blue}{\mbox{blue}}$ dot must be at the boundary delimiting the $\color{gray}{\mbox{gray}}$ area, which is the mapping
$(-1/2 < \xi < +1/2,-1/2 < \eta < + 1/2) \to (x,y)$ .
Free software source accompanying all this is found at my website .

