Error $\Delta A$ in Least Squares best fit of data to hyperbola $y=B/(x-A)$
Problem description.
Let there be given a set of real-valued data points $\,(x_i,y_i)\,$.
Find the Least Squares best fit of these points to a hyperbola $\;y = B/(x-A)\;$,
written as $\;y(x-A)-B=0\;$:
$$
\sum_i \left[\,y_i(x_i-A) - B\,\right]^2 = \mbox{minimum}(A,B)
$$
The minimum is found with help of partial differentiation, giving:
$$
\frac{\partial}{\partial A} \quad : \quad \left(\sum_i y_i^2\right) A + \left(\sum_i y_i\right) B = \sum_i x_i y_i^2 \\
\frac{\partial}{\partial B} \quad : \quad \left(\sum_i y_i\right) A + \left(\sum_i 1\right) B = \sum_i x_i y_i
$$
The solution of this system of linear equations is:
$$
A = \frac{M_{22}R_1-M_{12}R_2}{M_{11}M_{22}-M_{12}^2} \quad ; \quad
B = \frac{-M_{12}R_1+M_{11}R_2}{M_{11}M_{22}-M_{12}^2}
$$
With:
$$
M_{11} = \sum_i y_i^2 \quad ; \quad M_{12} = \sum_i y_i \quad ; \quad M_{22} = \sum_i 1 \\
R_1 = \sum_i x_i y_i^2 \quad ; \quad R_2 = \sum_i x_i y_i
$$
So far so good. We are especially interested in the value of $\,A\,$. But
what bothers us is the error / the uncertainty in $\,A\,$, let's call it $\,\Delta A\,$.
Pictures say more than a thousand words. The red line on the left is the asymptote of the hyperbola, at $\,A\,$.
In the same picture rightmost we see the data, enlarged for clarity in the picture on the right.
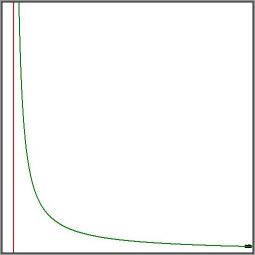
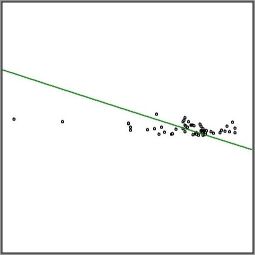
I really have no clue how to obtain a decent estimate for $\,\Delta A\,$ neither in theory or experimentally.
I'm afraid that it is bad. But anyway, any help is highly appreciated!



