A community project: prove (or disprove) that $\sum_{n\geq 1}\frac{\sin(2^n)}{n}$ is convergent

Elementary error analysis of a (neat) function $f(x)$ commonly proceeds as follows, with $\Delta f$ the error in $f$ and $\Delta x$ the error in its argument, everything real valued and positive. $$ \Delta f = \left| f'(x)\right| \Delta x $$ Now I know that we are not going to have such a neat function. But anything quick and dirty at this moment, objections / refinements later on please. Consider: $$ f(x) = \sum_{n\geq 1}\frac{\sin(x^n)}{n} $$ Rationale :   if   the series is convergent ,   then   in an incredibly small neighborhood of $\,x=2\,$ it should be convergent as well. Take the derivative (eventually assuming that the sum is finite and taking cautiously the "limit" for $n\to\infty$ afterwards): $$ \left| f'(x=2) \right| = \left| \sum_{n\geq 1}\frac{\sin'(x^n)}{n} \right| = \left| \sum_{n\geq 1} x^{n-1}\cos(x^n) \right| = \left| \frac{1}{2} \sum_{n\geq 1} 2^n\cos(2^n) \right| = \infty $$ Because it cannot be assumed that sufficient many terms $\,\cos(2^n)\,$ are zero. What does the above mean? It means that an infinitesimally small disturbance $\,\Delta x\,$ in $\,x=2\,$ leads to an infinitely large error in $f(x=2)$. Therefore any attempt to obtain a decent numerical approximation of the result will turn out to be merely futile.

I am not a mathematician. But, as a physicist by education, with some background in mumerical analysis, I find the question utterly absurd, as has been motivated with the humble means I have at my disposal. I firmly believe in the consistency of real world mathematics, especially calculus. If the error in an outcome is infinite, then it has no sense to even talk about it.

EDIT. Here is a little Pascal program that shows how the derivatives $f'_n(x=2)$ of the partial sums explode with increasing $n$ (even much wilder than I thought):

program Jack;

procedure main(n : integer);
var
  S,y : double;
  k : integer;
  m : Longint;
begin
  y := cos(1);
  S := 0; m := 1;
  for k := 1 to n do
  begin
    y := 2\*sqr(y)-1;
    m := m\*2;
    S := S + y\*m;
    Writeln(S/2);
  end;
end;

begin
  main(32);
end.

Output:

-4.16146836547142E-0001
-1.72343407827437E+0000
-2.30543421350882E+0000
-9.96671005609590E+0000
 3.38086371200828E+0000
 1.59202950857539E+0001
-2.84250375171363E+0001
-3.35182547883263E+0001
-2.88707602845465E+0002
 2.16817449683092E+0002
 1.18934540854247E+0003
 2.83591818496121E+0003
 4.03523441160830E+0003
-2.75211772559970E+0003
 3.35809567013370E+0003
-2.02949854476886E+0004
-1.75365217799296E+0004
-1.48144097841554E+0005
 1.10291092975492E+0005
 6.05118508207478E+0005
 1.42463158035994E+0006
 1.88943665520724E+0006
-1.89279657909947E+0006
 3.36118140293160E+0006
-2.53285957166623E+0005
-3.06929284003735E+0007
 1.26541774184908E+0007
-9.56811684138041E+0006
-2.63286281183089E+0008
 1.59073869302580E+0008
-9.62791988287838E+0007
-9.62791988287838E+0007

EDIT. Consider the sequence $\, c_n = \cos\left(2^n \phi\right)$. Question is why the sequence is seemingly random. I think the following can be said.  If  there is some structure in the iterands to be revealed ,  then  the only regularity one can think about is : periodicity . Now suppose that the sequence is indeed repeating, starting with some angle $\,0 \le \phi < \pi$ , then without loss of generality : $$ \cos\left(2^n \phi\right) = \cos\left(\phi\right) \quad \Longleftrightarrow \quad 2^n \phi = \begin{cases} k\cdot 2\pi - \phi \\ l\cdot 2\pi + \phi \end{cases} \quad \Longleftrightarrow \\ \phi = \begin{cases} k/(2^n+1)\cdot 2\pi \\ l/(2^n-1)\cdot 2\pi \end{cases} \quad \mbox{with} \quad \begin{cases} k = 0,1,2,\cdots ,2^{n-1} \\ l = 1,2,\cdots , (2^{n-1}-1) \end{cases} $$ The angle we start with is $\,\phi_0 = 1$ , so it can be assumed that for some positive integer $m$ : $\phi = \left|2^m - j\cdot 2\pi\right|\,$ with $\,j\,$ a positive integer such that $\,0 \le \phi < \pi$ . Also assume that $\,k > 0\;$ - thus skipping the trivial solution, then: $$ \left|2^m - j\cdot 2\pi\right| = \begin{cases} k/(2^n+1)\cdot 2\pi \\ l/(2^n-1)\cdot 2\pi \end{cases} \quad \Longleftrightarrow \quad \pi = \begin{cases} 2^{m-1} /\left[j\pm k/(2^n+1)\right] \\ 2^{m-1} /\left[j\pm l/(2^n-1)\right] \end{cases} $$ In any case the conclusion would be that $\,\pi\,$ is a fraction of positive integers, a rational number. But we know that $\,\pi\,$ is irrational. Hence the assumption that $\,c_n\,$ is repetitive leads to a contradiction. This proves that there is NO periodicity in the sequence; it is random in that sense.
But there is more. In the answer by user Alexander Rodin the argument of the sine - hence of our cosine - is defined apart from periodicity $= 2\pi\left\{\frac{2^n}{2\pi}\right\}$ . It is argued that the values of this variable are uniformly distributed. This has been schecked numerically and in an affirmative sense, by making a histogram of the values $0 \le x \le \pi$ as generated by:

x := 1; y := cos(x);
while true do
begin
  y := 2*sqr(y)-1; x := arccos(y);
end;

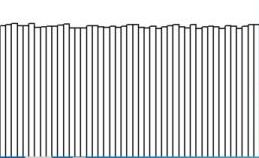
The result can be greatly improved by enlarging the amount of samples.

Too long for a comment. The function is not differentiable, I knew it would come ..
For the sake of simplicity, consider instead the Heaviside step function $\,u(t)$ : $$ u(t) = \begin{cases} 0 & \mbox{for} & t < 0\\ 1 & \mbox{for} & t > 0\end{cases} $$ The derivative of $\,u(t)\,$ is known to be the Dirac delta : $u'(t) = \delta(t)$ , so despite of the fact that the Heaviside is not differentiable for $\,t=0$ , it yet has a derivative there, which is $\,\infty$ . This is a clear signal that there is an error at $\,t=0\,$ that will not disappear with refined analysis.
Mind that I didn't even try to define $\,u(t)\,$ for $\,t=0$ . Because, as a physicist, I find that $\,u(t)$ , rather than well-defined, must be multi-valued at $t=0$ , i.e. it is not even a function there.
Now everybody can see immediately that the error in a multi-valued $\,u(0)\,$ is simply $= 1$ .