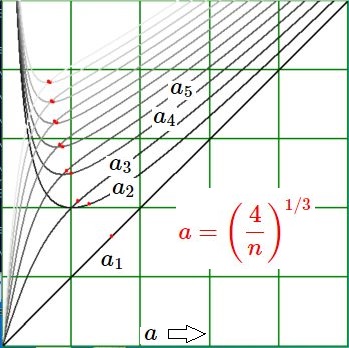
Prove conjecture $a_{n+1}>a_{n}$ if $a_{n+1}=a+\frac{n}{a_{n}}$

A picture says more than a thousand words. Successive iterands must be read from the bottom to the top, following e.g. one of the vertical green lines:

Thirteen functions $a_k(a)$ with $k = 1,2,\cdots ,13$ are displayed; lower iterands with darker lines.
The viewport is: 

xmin = 0; xmax = 5; ymin = 0; ymax = 5;
Let's make a few calculations, for the sake of understanding the graphics: $$ a_1(a) = a\\ a_2(a) = \frac{a^2+1}{a}\\ a_3(a) = \frac{a(a^2+3)}{a^2+1}\\ a_4(a) = \frac{a^4+6a^2+3}{a(a^2+3)}\\ a_5(a) = \frac{a(a^4+10a^2+15}{a^4+6a^2+3} $$ That's enough to see the folowing fact: It is also noticed that the numerator of $a_k(a)$ always becomes the denominator of $a_{k+1}(a)$.
It is seen that the curves [ $a_2(a)$ and $a_3(a)$ ] , [ $a_4(a)$ and $a_5(a)$ ] , [ $a_6(a)$ and $a_7(a)$ ] , in general
[ $a_{even}(a)$ and $a_{even+1/odd}(a)$ ] each have an intersection point. For [ $a_2(a)$ and $a_3(a)$ ] this point is easy to find: $$ a + \frac{1}{a} = a + \frac{2}{a + \frac{1}{a}} \quad \Longrightarrow \quad 2a = a + \frac{1}{a} \\ \Longrightarrow \quad (a,a_2(a))=(a,a_3(a))=(1,2) $$ But if we want to find some other intersection points, considerable difficulties cross our path; even the help of a computer algebra system (like MAPLE) seems to be futile, with exact solutions.
So let's take a look instead at the ingenious conjecture as proposed by the OP: $$ n > \frac{4}{a^3} \quad \Longrightarrow \quad a > \left(\frac{4}{n}\right)^{1/3} $$ These values $a$ together with their function values $a_k(a)$ are displayed as red dots in the picture.
It is clearly seen that the conjecture is quite good, especially for larger values of $n$.
It is an approximation, though, and a sufficient condition at best, not a necessary condition.
But in order to formulate a sufficient and necessary condition, the above mentioned intersection points must be found, which seems at this moment a too hard task to accomplish.

EDIT. In order to solve for the points of intersection, equate $a_{n+1}$ to $a_n$ , noticing that $a_n > 0$ : $$ a_n = a_{n+1} = a + \frac{n}{a_n} \quad \Longrightarrow \quad a_n^2-a\cdot a_n-n = 0 \quad \Longrightarrow \quad a_n = \frac{a}{2} + \sqrt{\left(\frac{a}{2}\right)^2+n} $$ So now we know the ordinates of the intersection points. But, unfortunately, that doesn't give us any information about the abscissas $a$. What we can do is draw the $\color{blue}{\mbox{graphs}}$ of the new functions, name them $b_n(a)$ :

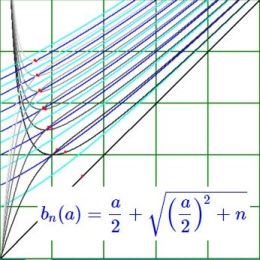
We expect that $b_n(a) = a_n(a) = a_{n+1}(a)$ at the intersection points. However, there is a difference between the curves in dark Blue and light blue (Aqua). The former are for $b_n(a)$ with $n = $ even; they intersect $a_n(a)$ and $a_{n+1}(a)$ as expected. The latter are for $b_n(a)$ with $n = $ odd; they do not intersect $a_n(a)$ and $a_{n+1}(a)$. But all blue curves $b_n(a)$ are somehow interesting, because they are asymptotes to the curves $a_n(a)$. For large values of $a$ we have almost straight lines: $$ b_n(a) = \frac{a}{2}+\frac{a}{2}\sqrt{1+\frac{n}{(a/2)^2}} \approx a + \frac{n}{a} $$ Still another way to calculate the intersection points is to determine the minimum of the curves $a_n(a)$ for $n = $ even. Which is easy to prove, because $a_n(a)\ne a/2$ in : $$ a_n^2(a)-a\cdot a_n(a)-n = 0 \quad \Longrightarrow \quad a_n'(a)\left[2 a_n(a)-a\right]= 0 \quad \Longrightarrow \quad a_n'(a)=0 $$ The slope of the accompanying odd curve at such a minimum is always $1$ , according to: $$ a_{n+1}'(a) = \left(a-\frac{n}{a_n(a)}\right)' = 1-\frac{n\, a_n'(a)}{a_n^2(a)} = 1 $$ Let's do some work with help of MAPLE: 

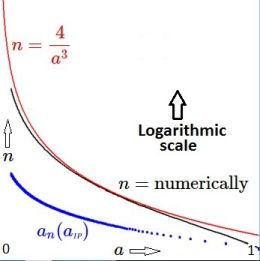
\> a_1 := a; a_2 := a+1/a_1; a_3 := a+2/a_2; a_4 := a+3/a_3; a_5 := a+4/a_4;

\> fsolve(a_4=a_5,a,0..infinity);

                             0.8713379136

\> fsolve(a_4=a/2+sqrt((a/2)^2+4),a,0..infinity);

                             0.8713379136

\> fsolve(diff(a_4,a)=0,a,0..infinity);

                             0.8713379136

\> subs(a=%,a_4);

                             2.482570870
Though I find it not very enlightning, in this case an exact solution can be found as well: $$ a_{4,5} = \sqrt{\left(8+6\sqrt{2}\right)^{1/3}-\frac{2}{\left(8+6\sqrt{2}\right)^{1/3}}-1}; $$ Continuing in this way (with some higher precision) gives the following results, before MAPLE and my own Newton-Raphson iterations give up. $$ \begin{matrix} {\bf \mbox{IP abscisssa} \; a} & {\bf n} & {\bf < 4/a^3} \\ 1 & 2,3 & 4 \\ 0.871337913570159 & 4,5 & 6.04644570004055 \\ 0.792253607266638 & 6,7 & 8.04391208677473 \\ 0.736268951824715 & 8,9 & 10.0219107501819 \\ 0.693502616556087 & 10,11 & 11.9926643644897 \\ 0.659225892899425 & 12,13 & 13.9623081896349 \\ 0.630825547822963 & 14,15 & 15.9342699607407 \\ 0.606713039185383 & 16,17 & 17.9105946558336 \end{matrix} $$ Herewith the conjecture is proved , for $\;n=1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17$ .

POST BOUNTY. Geromty's conjecture has been proved now (numerically) for $n$ up to $10,000$ . The only limitation seems to be that one has to halt at some place. Our last line of output has been: $$ \begin{matrix} {\bf \mbox{IP abscisssa} \; a} & {\bf n} & {\bf < 4/a^3} \\ 0.0564535548737650 & 9998,9999 & 22232.3877129834 \end{matrix} $$ It is thus noticed that geromty's formula gives over-estimates by more than a factor $2$ for such large values of $n$ , that is: if our calculations can be trusted. If one is truly interested in a lower bound for $n$ such that $\,a_{n+1} > a_n$ , then one could think about employing the little computer program below, instead of the conjecture. Here is the (Pascal) source code of the executable that does the job: 

program maple;

function quotient(n : integer; a : double) : double;
{
  a_n(x)/a_n'(x)
}
var
  x,y : double;
  k : integer;
begin
  y := a; x := 1;
  for k := 1 to n-1 do
  begin
    x := 1 - k\*x/sqr(y);
    y := a + k/y;
  end;
  quotient := (a + n/y - y)/(1 - n\*x/sqr(y) - x);
end;

procedure main(M : integer; var a : double);
{
  Newton-Raphson algorithm
}
var
  x,y : double;
begin
  x := a;
  while true do
  begin
    y := x;
    x := x - quotient(M,x);
    if abs(y - x) < 1.E-12 then Break;
  end;
  a := x;
end;

procedure test(M : integer);
var
  a,vgl : double;
  k : integer;
begin
  a := 1;
  for k := 2 to M do
  begin
    main(2\*k,a); vgl := 4/(a\*a\*a);
    Writeln(a,' ',2\*k,',',2\*k+1,' ',vgl);
  end;
end;

begin
  test(4999);
end.
I leave it up to the interested user to figure out the inner workings of this little program. Especially note that the quotient of $a_n(a)$ and its derivative $a_n'(a)$ can be calculated iteratively, in one sweep.

Upon request: A graph showing the (numerically obtained) intersection points (abscissas) as a function of $n$ would be nice :) But instead, here comes a graph of ( the natural logarithm of ) the number of iterations $n$ as a function of the abscissas $a$ of the intersection points, where $0 < a < 1$ and $0 < \ln(n) < 15$ . And $10,000$ intersection points have been taken into account.