The logarithm with base $2$ may be defined formally as $\,\operatorname{lg}(x) = \ln(x)/\ln(2)$ .
But in the practice below its meaning is much simpler, as might become clear from a few examples:
$\lg(2) = 1 \; ; \; \lg(4) = \lg\left(2^2\right) = 2 \; ; \; \lg(8) = \lg\left(2^3\right) = 3$ .
In general : $\,\operatorname{lg}\left(2^x\right) = x$ .
We need a function to chop off the exponent from a power (tower) of two.
We could have called this function "chopper", but the proper name for it in common mathematics is $2$-logarithm.
Take it, or if you don't like logarithms:
leave it. The whole employment of our "exponent chopper" is like in here: $2^x > 2^y \; \Longleftrightarrow \; x > y$ .
So what's the problem?
We are going to employ mathematical induction. To that end, define subsequent "approximations" of $A,B,C$ as follows: $$ A_n = a_{2n} \quad ; \quad B_n = b_{2n} \quad ; \quad C_n = c_{4n} $$ As the first induction step, we calculate: $$ A_1 = a_2 = 2^4 = 16 \quad ; \quad B_1= b_2 = 4^2 = 16 \quad ; \quad C_1 = c_4 = 2^{2^{2^2}} = 65536 $$ That's not enough to establish an inequality between $A$ and $B$, so we take a second step for these: $$ A_2 = a_4 = 2^{4^{2^4}} \quad ; \quad B_2 = b_4 = 4^{2^{4^2}} = 2^{2\cdot{2^{4^2}}} $$ Logarithms base $2$ : $$ \operatorname{lg}\left(2^{4^{2^4}}\right) = 4^{2^4} = 2^{2\cdot{2^4}} \quad ; \quad \operatorname{lg}\left(4^{2^{4^2}}\right) = 2\cdot 2^{4^2} = 2^{1+4^2} $$ And again: $$ \operatorname{lg}\left(4^{2^4}\right) = 2\cdot 2^4 = 32\quad ; \quad \operatorname{lg}\left(2\cdot 2^{4^2}\right) = 1 + 4^2 = 17 $$ From $\,32 > 17\,$ it follows that $\;A_2 > B_2\,$ , namely: $\;2^{2^{32}} > 2^{2^{17}}$ .
Now assume that $\;C_n > A_n > B_n \gg 1\;$ and prove that $\;C_{n+1} > A_{n+1} > B_{n+1}$ .
$$
\begin{matrix}
A_n = a_{2n} & B_n = b_{2n} & C_n = c_{4n} \\
A_{n+1} = a_{2n+2} = 2^{4^{A_n}} & B_{n+1} = b_{2n+2} = 4^{2^{B_n}} & C_{n+1} = c_{4n+4} = 2^{2^{2^{2^{C_n}}}}
\end{matrix}
$$
Taking logarithms two times:
$$
\begin{matrix}
\operatorname{lg}\left(A_{n+1}\right) = 4^{A_n} &
\operatorname{lg}\left(B_{n+1}\right) = 2\cdot 2^{B_n} &
\operatorname{lg}\left(C_{n+1}\right) = 2^{2^{2^{C_n}}} \\
\operatorname{lg}\left(\operatorname{lg}\left(A_{n+1}\right)\right) = 2A_n &
\operatorname{lg}\left(\operatorname{lg}\left(B_{n+1}\right)\right) = 1+B_n &
\operatorname{lg}\left(\operatorname{lg}\left(C_{n+1}\right)\right) = 2^{2^{C_n}} \end{matrix}
$$
From which it follows that $\;C_{n+1} > A_{n+1} > B_{n+1}\;$ as well. Especially:
$$
C_2 > A_2 > B_2
$$
So for all $\,n \ge 2\,$ we have $\;C_n > A_n > B_n$ . Now specialize for $\,n = 500\,$
and you're done.
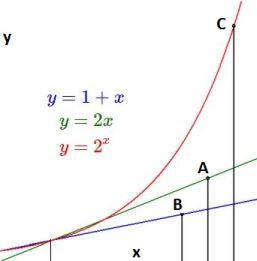
Conclusion : $\;C > A > B$ . Suggestive picture (not pretending anything more):

BONUS. Somewhat more of a challenge is the following modification of the question:
in $C$ there are $1500$ numbers $2$
(instead of $2000$). Then we have:
$$
A_n = a_{2n} \quad ; \quad B_n = b_{2n} \quad ; \quad C_n = c_{3n}
$$
And the first induction step results in an equality $\;A_1=B_1=C_1$ :
$$
A_1 = 2^4 = 16 \quad ; \quad B_1 = 4^2 = 16 \quad ; \quad C_1 = 2^{2^2} = 16
$$
A second step is needed to establish an inequality:
$$
\operatorname{lg}(\operatorname{lg}(A_2)) = 32 \quad ; \quad
\operatorname{lg}(\operatorname{lg}(B_2)) = 17 \\
\operatorname{lg}(\operatorname{lg}(C_2)) =
\operatorname{lg}\left(\operatorname{lg}\left(2^{2^{2^{16}}}\right)\right) =
\operatorname{lg}\left(2^{2^{16}}\right) = 2^{16} = 65536
$$
Finally resulting in the same as before: $\;C > A > B$ .