To begin with, a parallelogram $\overline{ABDC}$ is constructed inside a rectangle $\overline{AEDF}$:
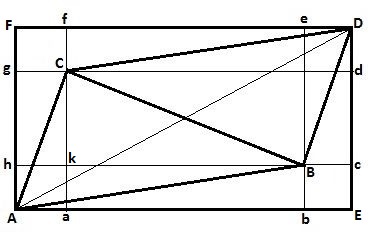
Label the vertices and assign a few coordinates (addition of vectors giving $D$): $$ A = (0,0) \quad , \quad B = (x_1,y_1) \quad , \quad C = (x_2,y_2) \quad \Longrightarrow \quad D = (x_1+x_2,y_1+y_2)$$ Then calculate areas according to the following, leaving it to the user to prove things where they feel the need. Though, with Euclidean geometry, What you see is what you get, most of the time: $$ \operatorname{Area}(\overline{CDf}) = \operatorname{Area}(\overline{AbB}) = \frac{1}{2} \operatorname{Area}(\overline{AbBh}) = \frac{1}{2} \overline{Ab}\times\overline{Ah} = \frac{1}{2} x_1y_1 \\ \operatorname{Area}(\overline{BcD}) = \operatorname{Area}(\overline{ACg}) = \frac{1}{2} \operatorname{Area}(\overline{AaCg}) = \frac{1}{2} \overline{Aa}\times\overline{Ag} = \frac{1}{2} x_2y_2 \\ \operatorname{Area}(\overline{bEcB}) = \operatorname{Area}(\overline{gCfF}) = \operatorname{Area}(\overline{Aakh}) = \overline{Aa}\times\overline{Ah} = x_2y_1 $$ Now subtract the areas of $\overline{AbB} , \overline{bEcB} , \overline{BcD} , \overline{CDf} , \overline{gCfF} , \overline{ACg}$ from the area of the big rectangle, which is $\operatorname{Area}(\overline{AEDF}) = (x_1+x_2)(y_1+y_2)$. Then what we get is the area of the parallelogram: $$ \operatorname{Area}(\overline{ABDC}) = (x_1+x_2)(y_1+y_2) - 2 x_2y_1 - 2\cdot\frac{1}{2} x_2y_2 - 2\cdot\frac{1}{2} x_1y_1 =\\ x_1y_1+x_1y_2+x_2y_1+x_2y_2 - x_2y_2 - x_1y_1 - 2x_2y_1 = x_1y_2-x_2y_1 $$ Do we observe a determinant here? Ayway, the area of the triangle is half of this: $$ \operatorname{Area}(\overline{ABC}) = \frac{1}{2}(x_1y_2-x_2y_1) = \frac{1}{2} \begin{vmatrix} x_1 & y_1 \\ x_2 & y_2 \end{vmatrix} $$ There are many interesting applications. For example, the area of an arbitrary polygon can be calculated with addition and subtraction of nothing else but triangles, as exemplified here. However, there is a tag (definite-integrals) associated with the question, so let's kill the mosquito with a gun end employ some of that in the end: $$ \operatorname{Area}(\overline{ABC}) = \operatorname{Area}(\overline{AaC}) + \operatorname{Area}(\overline{abBC}) - \operatorname{Area}(\overline{AbB}) =\\ \int_0^{x_2} \frac{y_2}{x_2}x\,dx \; + \; \int_{x_2}^{x_1} \left[y_2 + (y_1-y_2)\frac{x-x_2}{x_1-x_2} \right] dx \; - \; \int_0^{x_1} \frac{y_1}{x_1}x\,dx = \\ \frac{1}{2}x_2y_2 + \frac{1}{2}(x_1-x_2)(y_2+y_1)-\frac{1}{2}x_1y_1 = \frac{1}{2}(x_1y_2-x_2y_1) $$ Always nice to see the consistency of mathematics showing up again.