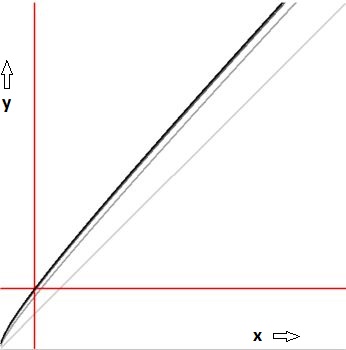
To what function does this series converge?
Very much partial answer. Here is a graph of the function
$$
y = f(x) = \sum_{n=1}^N \frac{1}{n!} x^{1/n} \quad ; \quad 0 < x,y < 10
$$
Convergence is quickly.
The more converged (ipse est larger values of $\,N\,$) the darker the drawings.
One of the few things one can say is that the function goes through the point $\,\color{red}{(x,y) = (1,e-1)}$ .