Catenary curve for minimum surface of revolution

Relevant references:

According to the first reference, the area of a surface of revolution is given by: $$ A_x=2\pi \int _{a}^{b} y(x) \sqrt {1+\left({\frac{dy}{dx}}\right)^2}\,dx $$ According to the second reference, the Euler-Lagrange equations, resulting from minimizing this area, are given by: $$ \frac{\partial L}{\partial q_k} - \frac{d}{dt} \left(\frac{\partial L}{\partial \dot{q}_k}\right) = 0 $$ In our case there is only one such equation: $$ \frac{\partial L}{\partial y} - \frac{d}{dx} \left(\frac{\partial L}{\partial y'}\right) = 0 \qquad \mbox{with} \qquad L(y,y') = y \sqrt {1+\left(y'\right)^2} $$ Here goes: $$ \frac{\partial L}{\partial y} = \sqrt{1+\left(y'\right)^2} \quad ; \quad \frac{\partial L}{\partial y'} = \frac{y\, y'}{\sqrt{1+\left(y'\right)^2}}\\ \frac{\partial L}{\partial y} - \frac{d}{dx}\frac{\partial L}{\partial y'} = \frac{\left[1+\left(y'\right)^2\right]^2}{\left[1+\left(y'\right)^2\right]^{3/2}} - \frac{\left[\left(y'\right)^2+y\,y''\right]\left[1+\left(y'\right)^2\right] - y\,\left(y'\right)^2\,y''} {\left[1+\left(y'\right)^2\right]^{3/2}} = 0 $$ Simplification results in the following ODE: $$ 1 + (y')^2 - y\cdot y'' = 0 \qquad \mbox{or} \qquad y\cdot y'' - (y')^2 = 1 $$ The Ansatz $\;y(x) = a\cdot \cosh(x/a+b)\;$ with $(a,b)$ real constants results in the same structure: $$ \left[a\cdot \cosh(x/a+b)\right]\left[a\cdot \cosh''(x/a+b)\right] - \left[a\cdot \cosh'(x/a+b)\right]^2 = \\ = \cosh^2(x/a+b) - \sinh^2(x/a+b) = 1 $$ We conclude that the catenoid with $\;y(x) = a\cdot \cosh(x/a+b)\;$ is a solution.
(The present approach does not reveal if that solution is the only one, though)

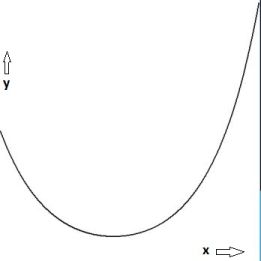
Boundary conditions. Indeed, given two fixed points in plane, we can hang catenaries of different length. Mathematically, this is expressed by $\;y(x) = A\cosh(Bx+C)\;$ with three constants $\,(A,B,C)$ . Apart from the two fixed points, this enables the length to become an additional degree of freedom.
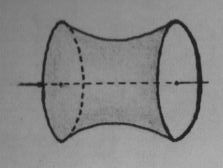
The situation is different with the catenoid. Instead of three constants $\,(A,B,C)\,$ we have only two of these : $(a,b)$ . A physical consequence is that there is only one soap film between two rings:

Mathematics please. So let's try to solve for $\,(a,b)$ , given the fixed points $\,(x_1,y_1),(x_2,y_2)$ : $$ \begin{cases}y_1 = a\,\cosh(x_1/a+b) \\ y_2 = a\,\cosh(x_2/a+b) \end{cases} $$ Two equations with two unknowns. Doing it by hand seems to be hopeless. Feeding it into my favorite computer algebra system (MAPLE) results in a two page long expression that the OP doesn't want to know, I think.
Anyway, the length $L$ of the soapfilm catenary can be expressed in the solutions $\,(a,b)\,$ and the abscissae of the end-points, therefore it is no longer a degree of freedom: $$ L = \int_{x_1}^{x_2} \sqrt{1+\left[y'(x)\right]^2}\,dx = \int_{x_1}^{x_2} a\sqrt{1+\left[\sinh(x/a+b)\right]^2}\,d(x/a+b) \\ = \int_{x_1/a+b}^{x_2/a+b} a\cosh(u)\,du = a\sinh(x_2/a+b)-a\sinh(x_1/a+b) $$ Brute force. Numerical methods may offer a panacea where analytical methods fail. For ease of the calculations, replace $\,b\,$ by $\,(-p/a)\,$ - should have done this from the beginning - and consider instead: $$ \begin{cases}y_1 = a\,\cosh((x_1-p)/a) \\ y_2 = a\,\cosh((x_2-p)/a) \end{cases} $$ Then $\,x = p\,$ is the place where the catenary has its the minimum $\,a$ . It follows that, without loss of generality (??) : $x_1 \le p \le x_2\,$ and $\,0 < a \le \min(y_1,y_2)\,$ . With the home-made tools I have at my disposal, I can easily make an isoline chart / contour plot of the place where the following functions are zero: $$ \begin{cases} \color{red}{f(p,a) = a\,\cosh((x_1-p)/a)-y_1 = 0} \\ \color{green}{g(p,a) = a\,\cosh((x_2-p)/a) - y_2 = 0} \end{cases} $$ Now determine numerically the intersection point of the green and red isolines and you're done.

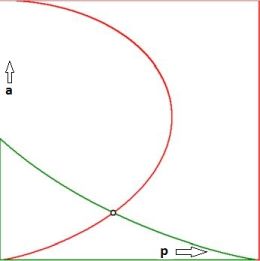
An example with $(x_1,y_1) = (1,1)$ and $(x_2,y_2) = (2,2)$ results in the following values of $(p,a)$:

1.43600867678959E+0000 1.82608695652174E-0001

And the catenary of the catenoid can be sketched with these values, at last: