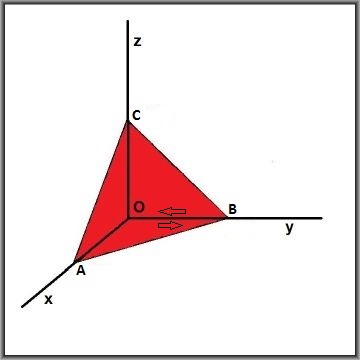

Thanks to Green's theorem we can replace area integrals by line-integrals; mind that they are counter-clockwise.
Then it is clear that, irrespective of any further content:
$$
\oint_{OAB} + \oint_{OBC} + \oint_{OAC} + \oint_{ABC} = 0
$$
Assuming that the operator rot(ation) is not defined yet in general, this means that we now have an expression for it:
$$
2 \iint_{ABC} \vec{\operatorname{rot}}(\vec{F}) \cdot \vec{n}\, dA = \\
- \iint_{xy} \left(\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}\right) dx\, dy
- \iint_{yz} \left(\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}\right) dy\, dz
- \iint_{zx} \left(\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}\right) dz\, dx
$$
Continuing with infinitesimal volumes / areas and flipping normals on the right hand side, so that they become
the components of the normal at the left hand side:
$$
\vec{\operatorname{rot}}(\vec{F}) \cdot \vec{n}\, \Delta A = \\
\left(\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}\right)\cdot n_x\, \Delta A +
\left(\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}\right)\cdot n_y\, \Delta A +
\left(\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}\right)\cdot n_z\, \Delta A
$$
Leaving out the infinitesimal area $\,\Delta A\,$ gives us the same answer as found by the OP themselves.
A somewhat neater approach is to calculate mean values and let the area of the (red) triangle go to zero:
$$
\vec{\operatorname{rot}}(\vec{F}) \cdot \vec{n} = \lim_{ABC \to 0}
\frac{\iint_{ABC} \vec{\operatorname{rot}}(\vec{F}) \cdot \vec{n}\, dA}{\iint_{ABC} dA}
$$
Note. I've encountered essentially the same method at several places elsewhere in physics
(I think it's with stress and strain). Aanyway, a related subject is :
What does shear mean?