Maximum value $c$ s.t. $\exists$ a subset $S$ of $\{z_1,z_2,\ldots,z_n\}$ s.t. $\left|\sum_{z\in S}z\right|\geq c$ ($\sum_{i=1}^{n}|z_i|=1$).

Special case first. It is supposed that the maximum value $\,c\,$ is achieved for evenly distributed $\{z_0,z_1,\ldots,z_{n-1}\}$ . This means that $$ z_k = \frac{1}{n} e^{i\cdot k\,2\pi/n} \quad \Longrightarrow \quad |z_0|+|z_1|+\cdots +|z_{n-1}|=1 $$ Easy results are obtained (by hand) for $n=1,2,3,4$: $$ \begin{cases} n=1 \quad \Longrightarrow \quad S = \{1\} & \mbox{and} & \left|\sum_{z\in S} z\right|\geq 1 > 1/\pi \\ n=2 \quad \Longrightarrow \quad S = \{1/2\} & \mbox{and} & \left|\sum_{z\in S} z\right|\geq 1/2 > 1/\pi \\ n=3 \quad \Longrightarrow \quad S = \{1/3,(-1-i\sqrt{3})/6\} & \mbox{and} & \left|\sum_{z\in S} z\right|\geq 1/3 > 1/\pi\\ n=4 \quad \Longrightarrow \quad S = \{1/4,i/4\} & \mbox{and} & \left|\sum_{z\in S} z\right|\geq \sqrt{2}/4 > 1/\pi \end{cases} $$ This already improves the bounds $1/6$ and $1/4$ as given in the question (at best for $n=3$).
Higher order results are obtained with help of a computer program. The lines giving $n$ , $\left|\sum_{z\in S} z\right|$ and $1/\pi$ are alternating with lines giving the indices $\,k\,$ of the terms $\,z_k\,$ in the sum $\,\left|\sum_{z\in S} z\right|$ .
It is shown that the sums indeed seem to converge to the conjectured value of $1/\pi$ . And there is a pattern in the subsets that do the job. 
    1 1.00000000000000E+0000 >  3.18309886183791E-0001
0 
    2 5.00000000000000E-0001 >  3.18309886183791E-0001
0 
    3 3.33333333333333E-0001 >  3.18309886183791E-0001
0 2 
    4 3.53553390593274E-0001 >  3.18309886183791E-0001
0 1 
    5 3.23606797749979E-0001 >  3.18309886183791E-0001
0 1 2 
    6 3.33333333333333E-0001 >  3.18309886183791E-0001
0 4 5 
    7 3.20997086245352E-0001 >  3.18309886183791E-0001
0 1 2 
    8 3.26640741219094E-0001 >  3.18309886183791E-0001
0 1 2 3 
    9 3.19931693507980E-0001 >  3.18309886183791E-0001
5 6 7 8 
   10 3.23606797749979E-0001 >  3.18309886183791E-0001
3 4 5 6 7 
   11 3.19394281060558E-0001 >  3.18309886183791E-0001
4 5 6 7 8 9 
   12 3.21975275429689E-0001 >  3.18309886183791E-0001
1 2 3 4 5 6 
   13 3.19085761944568E-0001 >  3.18309886183791E-0001
3 4 5 6 7 8 
   14 3.20997086245352E-0001 >  3.18309886183791E-0001
0 1 2 3 4 5 6 
   15 3.18892407783521E-0001 >  3.18309886183791E-0001
0 1 2 3 11 12 13 14 
   16 3.20364430967688E-0001 >  3.18309886183791E-0001
0 1 2 3 4 13 14 15 
   17 3.18763277866454E-0001 >  3.18309886183791E-0001
5 6 7 8 9 10 11 12 
   18 3.19931693507980E-0001 >  3.18309886183791E-0001
2 3 4 5 6 7 8 9 10 
   19 3.18672778564237E-0001 >  3.18309886183791E-0001
2 3 4 5 6 7 8 9 10 
   20 3.19622661074983E-0001 >  3.18309886183791E-0001
3 4 5 6 7 8 9 10 11 12 
   21 3.18606904753685E-0001 >  3.18309886183791E-0001
0 1 2 3 15 16 17 18 19 20 
   22 3.19394281060558E-0001 >  3.18309886183791E-0001
0 1 2 3 4 5 6 7 8 9 10 
   23 3.18557468338846E-0001 >  3.18309886183791E-0001
7 8 9 10 11 12 13 14 15 16 17 
   24 3.19220732314183E-0001 >  3.18309886183791E-0001
4 5 6 7 8 9 10 11 12 13 14 15
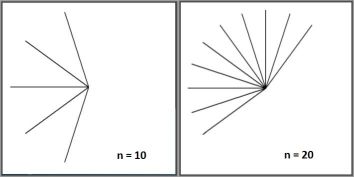
Two snapshots should clarify the pattern in the subsets that do the job:

So it seems that, without too much loss of generality, we can conjecture that: $$ \left|\sum_{z\in S} z\right| = \left|\sum_{k=0}^{n/2-1} \frac{1}{n} e^{i\cdot k\,2\pi/n}\right| $$ The sum of a geometric series is recognized herein: $$ \sum_{z\in S} z = \frac{1}{n} \frac{1-r^{n/2}}{1-r} \quad \mbox{with} \quad r = e^{i\cdot 2\pi/n} $$ Hence: $$ \left|\sum_{z\in S} z\right| = \frac{1}{n} \left|\frac{1-e^{i\cdot 2\pi/n\cdot n/2}}{1-e^{i\cdot 2\pi/n}}\right| = \frac{1}{n} \left|\frac{2\cdot i}{e^{i\cdot \pi/n}\left(e^{-i\cdot \pi/n}-e^{i\cdot \pi/n}\right)\cdot i}\right| = \frac{\pi/n}{\sin(\pi/n)}\frac{1}{\pi} $$ And a well known limit tells us that $$ \lim_{n\to\infty} \left|\sum_{z\in S} z\right| = \frac{1}{\pi} $$ in concordance with the numerical experiments.
Don't get me wrong. The above is only a sketch of a proof. Quite some technicalities remain to be filled in. The main part to be proved is: why should this very special case be relevant for the general case of arbitrary $\,z_k$ ? (Though it's not uncommon that solutions of high symmetry are relevant for finding extreme values in a more general setting)