
GEOMETRICAL ALGEBRA.
We have already seen [ .. ] how the Pythagoreans and later Greek mathematicians exhibited different kinds of numbers as forming different geometrical figures. [ skip text ] The product of two numbers was thus represented geometrically by the rectangle contained by the straight lines representing the two numbers respectively. It only needed the discovery of incommensurable or irrational straight lines in order to represent geometrically by a rectangle the product of any two quantities whatever, rational or irrational; and it was possible to advance from a geometrical arithmetic to a geometrical algebra, which indeed by Euclid’s time (and probably long before) had reached such a stage of development that it could solve the same problems as our algebra so far as they do not involve the manipulation of expressions of a degree higher than the second. [ rest deleted ]
As quoted from the second reference:
Descartes began by interpreting the algebraic operations of addition, subtraction, multiplication, division,
and extraction of square roots as geometric constructions on lines. He represented each (positive) magnitude
by a line. Addition and subtraction were the same as Euclid’s. To add two lines, just extend one by the length
of the other. To subtract one line from another, just take the remainder after cutting it off the other.
Multiplication and division, however, were different from Euclid’s. Euclid represented the product of two lines
by a rectangle, the product of three lines by a box in space, and Euclid didn’t represent the product of four lines.
But Descartes took the product of two lines to be another line. [emphasis is mine] That required selecting a unit line,
that is, a line of length $1$. Then to find the product $ab$ of two quantities $a$ and $b$, he only needed to find
the fourth proportional of $1$, $a$, and $b$.
Here is the construction by Descartes (figure on the left):
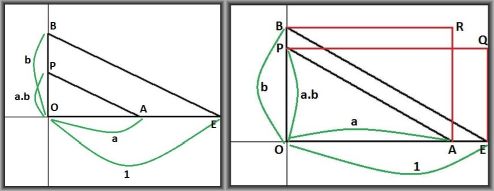
After defining a unit OE and the lengths (= reals) OA and OB, in order to define the product OP, it is necessary
to draw a line OP parallel to EB.
Of course, there is a relationship between Euclid's and Descartes' construction: the areas of OARB and OEQP are equal.
It should be noted though, that negative numbers are impossible within Euclid's system, while the (Des)Cartesian
coordinate system ensures that they can be properly represented geometrically.
Why is negative times negative = positive?
Descartes' Euclidean Geometrical Algebra gives us a nice proof without words :
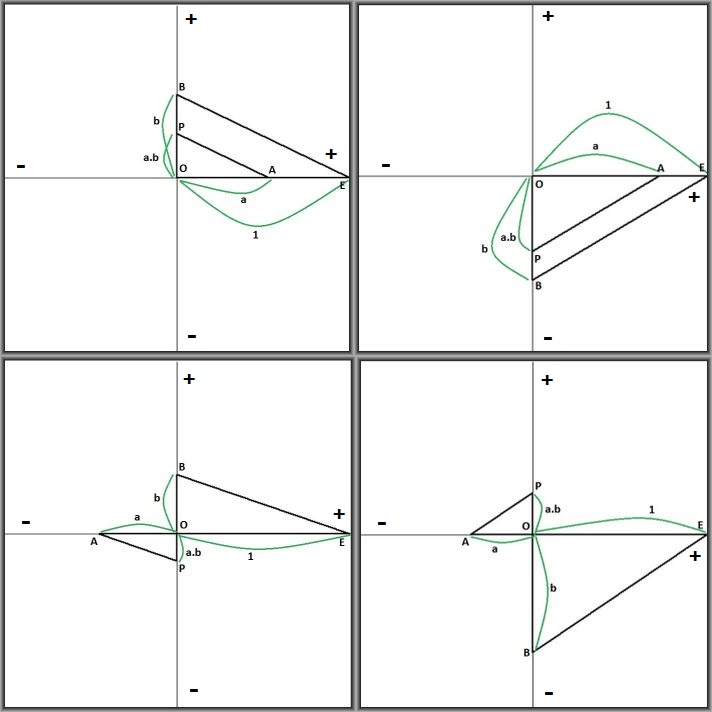
Parallel lines seem to be essential all over the place, thus requiring an Euclidean geometry.
And doesn't our common Equals sign not just represent two parallel $=$ lines?
So the question is: does there exist a multiplication of reals a la Descartes in a
non-Euclidean Geometrical Algebra ?
Possible duplicate question, without an answer :
Geometric basis for the real numbers .