Division of regular tetrahedron
As already pointed out in a comment by Moishe Cohen and especially
the comment by Alex Ravsky, the answer is negative. Let attention
be restricted to the regular tetrahedron: dividing the length of each edge by two would result in $2^3 = $ eight smaller instances
of that regular tetrahedron. Suppose that we try to assemble the original shape with these smaller tetrahedrons, placing four of
the $1/8$ ones at the corners of the original to begin with. Then there will be a void in the middle which has the shape of a regular
_octahedron_. It is impossible to fill that void with the remaining four smaller tetrahedrons. I have no rigorous proof for this,
but that doesn't serve as a disclaimer. Just use your imagination and you shall see:
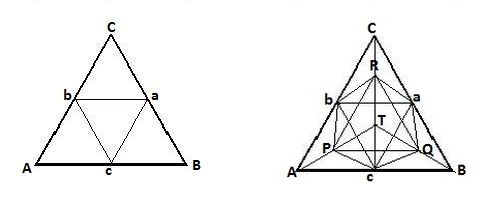
The simplified 2-D case is shown in the picture on the left. The picture on the right is the top view of a 3-D wire frame model of the
subdivided regular tetrahedron. The four smaller ones at the corners of the original shape ABCT are: AcbP , BacQ , CbaR at the bottom and PQRT at the first floor.
