$x,y,z \geqslant 0$, $x+y^2+z^3=1$, prove $x^2y+y^2z+z^2x < \frac12$

The method to be employed here is exactly the same as in a previous answer:

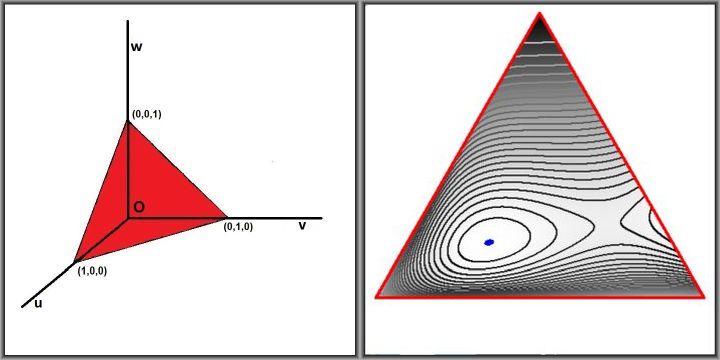
Let $u = x$ , $v = y^2$ , $w = z^3$ , then $u,v,w \ge 0$ , $u+v+w=1$ and the inequality to be established: $$ x^2y+y^2z+z^2x < \frac12 \quad \Longrightarrow \quad f(u,v,w) = u^2v^{1/2}+v\,w^{1/3}+w^{2/3}u < \frac12 $$ The maximum of this function inside the equilateral triangle must shown to be less than $1/2$.
There is no symmetry argument, because the latter is effectively destroyed by the "weird" condition $x+y^2+z^3=1$ , as it is called. Another proof without words is attempted by plotting a contour map of the function, as depicted. Levels (`nivo`) of these isolines are defined (in Delphi Pascal) as: 
nivo := min + sqrt(g/grens)*(max-min); { sqrt = square root ; grens = 25 ; g = 0..grens }
The darkness of the isolines is proportional to the (positive) function values; they are almost black near the maximum and almost white near the minimum values. Maximum and minimum values of the function are observed to be: 
 4.58251457205350E-0003 < f < 4.85621276951755E-0001 < 1/2
The little $\color{blue}{\mbox{blue}}$ spot is where $\left|f(u,v,w) - \mbox{max}\right|< 0.0002$ . This maximum is close to values found by other people here, but not quite. Perhaps it's interesting to know the position of the maximum as well: 
(x,y,z) = ( 5.58304528246164E-0001 , 4.97693736095187E-0001 , 5.78892473099889E-0001 )
I have no idea how to convert these numerical values into something more analytical.

EDIT. What you see is what you get :-) Without doubt. Some decent error analysis reveals that the value of the maximum to be trusted in this answer is : $\;0.48562 \pm 0.00003\;$ , quite in agreement with values given elsewhere (e.g. in the comment by Steve Kass).