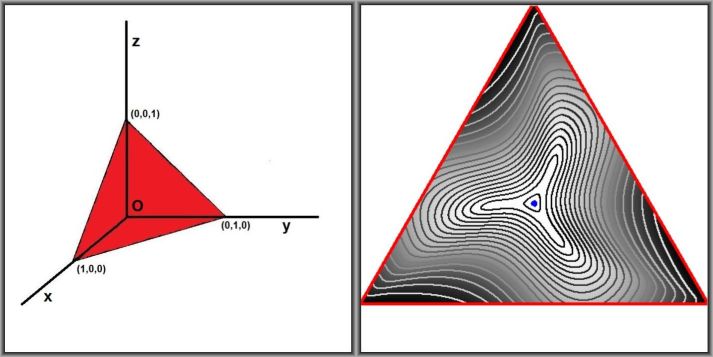
This is a question of the symmetric type, such as listed in:
With a constraint $\;x+y+z=1\;$ and $\;x,y,z > 0$ . Sort of a general method to transform such a into the inside of a triangle in 2-D has been explained at length in:Our function $f$ in this case is: $$ f(x,y,z) = \frac{x^4}{8x^3+5y^3}+\frac{y^4}{8y^3+5z^3}+\frac{z^4}{8z^3+5x^3} - \frac{1}{13} $$ And the minimum of that function inside the abovementioned triangle must shown to be greater or equal to zero. Due to symmetry - why oh why can it not be proved with Group Theory - an absolute minimum of the function is expected at $(x,y,z) = (1/3,1/3,1/3)$. Another proof without words is attempted by plotting a contour map of the function, as depicted. Levels (`nivo`) of these isolines are defined (in Delphi Pascal) as:
nivo := min + sqr(g/grens)*(max-min); { sqr = square ; grens = 20 ; g = 0..grens }
The whiteness of the isolines is proportional to the (positive) function values; they are almost black near the minimum and almost white near the maximum values.
Maximum and minimum values of the function are observed to be:
0.00000000000000E+0000 < f < 4.80709198767699E-0002The little $\color{blue}{\mbox{blue}}$ spot in the middle is where $\,0 \le f(x,y,z) < 0.00002$ .