Define:
$$
x = \frac{a^{3/4}}{2^{3/4}} = \left(\frac{a}{2}\right)^{3/4} \quad ; \quad
y = \frac{b^{3/4}}{2^{3/4}} = \left(\frac{b}{2}\right)^{3/4} \quad ; \quad
z = \frac{c^{3/4}}{2^{3/4}} = \left(\frac{c}{2}\right)^{3/4}
$$
Then:
$$
a = 2\,x^{4/3} \quad ; \quad b = 2\,y^{4/3} \quad ; \quad c = 2\,z^{4/3}
$$
And:
$$
\left(a^4\right)^{3/4} = a^3 = 2^3 x^4 \quad ; \quad
\left(b^4\right)^{3/4} = b^3 = 2^3 y^4 \quad ; \quad
\left(c^4\right)^{3/4} = c^3 = 2^3 z^4
$$
Finally, when $x,y,z > 0$, prove:
$$
f(x,y,z) =
\frac{2^3 x^4}{\left(2^3 x^4 + 2^3 y^4\right)^{3/4}} +
\frac{2^3 y^4}{\left(2^3 y^4 + 2^3 z^4\right)^{3/4}} +
\frac{2^3 z^4}{\left(2^3 z^4 + 2^3 x^4\right)^{3/4}} \ge 1
$$
Where it can be assumed without loss of generality that: $\,x+y+z = 1$ .
The problem is thus reduced to a familiar one, quite similar to:
And can be treated accordingly:
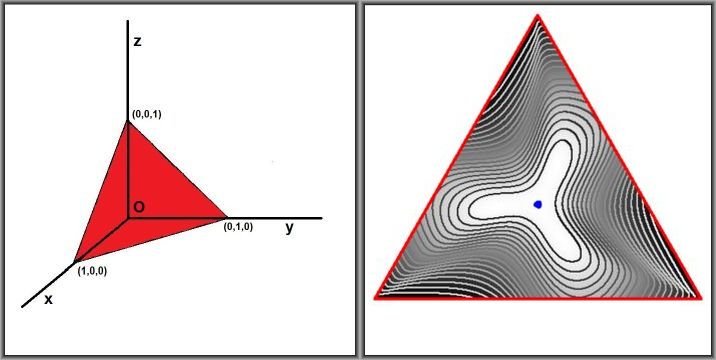
The minimum of our function inside the abovementioned triangle must shown to be greater or equal to one.
Another proof without words is attempted
by plotting a contour map of the function, as depicted. Levels (`nivo`) of these isolines are defined (in Delphi Pascal) as:
nivo := min + g/grens*(max-min); { grens = 20 ; g = 1..grens }
The whiteness of the isolines is proportional to the (positive) function values; they are almost black near the minimum and almost white near the maximum values.
Maximum and minimum values of the function are observed to be:
1.00001285611974E+0000 < f < 1.68177794816992E+0000
The little $\color{blue}{\mbox{blue}}$ spot in the middle is where $\,\left| f(x,y,z) - 1 \right| < 0.001$ . Due to symmetry,
an absolute minimum of the function is expected indeed at $(x,y,z) = (1/3,1/3,1/3)$.
Note.
Conditions similar to $\;x+y+z=1\;$ often occur in these inequalities, whether that is explicitly or implicitly.
An explicit example has been provided with another
HN_NH question :
Prove $\frac{xy}{5y^3+4}+\frac{yz}{5z^3+4}+\frac{zx}{5x^3+4} \leqslant \frac13$
The current inequality is an example of implicit occurrence. Let the function $f(x,y,z)$
be defined as above, then we have the equivalent inequality $\;f(x,y,z) \geqslant x+y+z$ .
It is clear that $f$ has the following property for all real $\lambda > 0$ :
$\;f(\lambda x,\lambda y,\lambda z) = \lambda f(x,y,z) \geqslant \lambda (x+y+z)$ .
Therefore $\lambda$ has no influence whatsoever on the inequality being true or false; we can always divide $x,y,z$ by a factor $\lambda$ such that $x+y+z=1$ .
Thus enabling a triangle mapping method once again.

