Dirac Delta Test Functions
Relevant References (MSE):
All functions defined on the reals and real valued.
Example 1. $T(x) =$ square:
$$
T(x) = \begin{cases} 0 & \mbox{for} & -\infty < x < -1/2 \\
1 & \mbox{for} & -1/2 < x < +1/2 \\ 0 & \mbox{for} & +1/2 < x < + \infty\end{cases}\\
\int_{-\infty}^{+\infty} T(x) \, dx = \mbox{area of } 1\times 1 \mbox{ square} = 1
$$
Sketch:
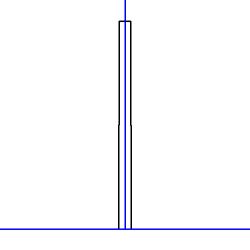
Example 2. $T(x) =$ triangle:
$$
T(x) = \begin{cases} 0 & \mbox{for} & -\infty < x < -1 \\
1+x & \mbox{for} & -1 < x < 0 \\ 1-x & \mbox{for} & 0 < x < +1 \\
0 & \mbox{for} & +1 < x < + \infty\end{cases}\\
\int_{-\infty}^{+\infty} T(x) \, dx = \mbox{area of triangle base } 2 \mbox{ height } 1 = 1
$$
Sketch:
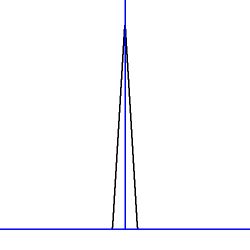
Helper function (Heaviside step):
$$
u(x) = \begin{cases} 0 & \mbox{for} & x < 0\\ 1 & \mbox{for} & x > 0\end{cases}
$$
Example 3. $T(x) =$ exponential, two versions:
$$
T_a(x) = u(x) e^{-x}\\
\int_{-\infty}^{+\infty} T_a(x) \, dx = \int_{0}^{+\infty} e^{-x} \, dx = \left[ - e^{-x} \right]_0^{\infty} = 1
$$ $$
T_b(x) = e^{-|x|}/2\\
\int_{-\infty}^{+\infty} T_b(x) \, dx = 2\int_{0}^{+\infty} T_a(x) \, dx / 2 = 1
$$
Sketch:
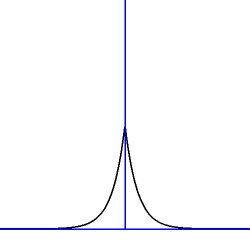
Example 4. $T(x) =$ Gaussian (normal distribution):
$$
T(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2}
$$
The proof that $\int_{-\infty}^{+\infty} T(x) \, dx = 1$ is so nice that it shall be reproduced here:
$$
\left(\int_{-\infty}^{+\infty} e^{-x^2/2} \, dx\right)^2 =
\int_{-\infty}^{+\infty} e^{-x^2/2} \, dx \cdot \int_{-\infty}^{+\infty} e^{-y^2/2} \, dy =\\
\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} e^{-(x^2+y^2)/2} \,dx\,dy =
\int_{r=0}^\infty \int_{\phi=0}^{2\pi} e^{-r^2/2} r\,dr\,d\phi =\\
\int_0^\infty e^{-r^2/2} \,d(r^2/2)\cdot\int_0^{2\pi}\,d\phi = \left[-e^{-x}\right]_0^\infty\cdot2\pi = 2\pi
\\ \Longrightarrow \quad \int_{-\infty}^{+\infty} e^{-x^2/2} \, dx = \sqrt{2\pi} \quad \mbox{Q.E.D.}
$$
Sketch:
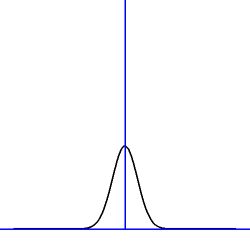
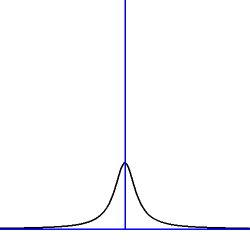
Example 5. $T(x) =$ Cauchy distribution:
$$
T(x) = \frac{1/\pi}{1+x^2}\\
\int_{-\infty}^{+\infty} \frac{1}{1+x^2} \, dx = \left[\,\arctan(x)\,\right]_{-\infty}^{+\infty} = \pi \quad \mbox{Q.E.D.}
$$
Sketch:
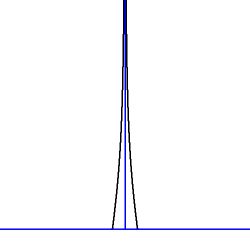
Example 6. $T(x) = $ infinite at $x=0$ with compact support, two versions:
$$
T_a(x) = \begin{cases} 0 & \mbox{for} & -\infty < x < 0 \\
(1-x)/\sqrt{1-(1-x)^2} & \mbox{for} & 0 < x < 1 \\
0 & \mbox{for} & 1 < x < +\infty \end{cases}
$$
Heuristics. Imagine a quarter of a circle with midpoint $(+1,-1)$ and radius $=1$.
The tangent at $(0,-1)$ is $+\infty$ and the tangent at $(+1,0)$ is $0$. The equation
of the circle is $\,(x-1)^2+(y+1)^2=1$ . It follows that $\,y(x) = -1 \pm \sqrt{1-(1-x)^2}$ .
Now take the derivative of this and obtain $T(x) = y'(x)$ for $\,0 < x < 1$ . It's easy to
calculate the normed integral:
$$
\int_{-\infty}^{+\infty} T_a(x) \, dx = \int_0^1 y'(x) \, dx = \left[-1 + \sqrt{1-(1-x)^2}\right]_0^1 = 1
$$
Symmetric version $\,T_b(x)=\left[T_a(x)+T_a(-x)\right]/2$ :
$$
T_b(x) = \begin{cases} 0 & \mbox{for} & -\infty < x < -1 \\
(1-|x|)/\sqrt{1-(1-|x|)^2}/2 & \mbox{for} & -1 < x < +1 \\
0 & \mbox{for} & +1 < x < +\infty \end{cases}\\
\int_{-\infty}^{+\infty} T_b(x) \, dx = 2\int_0^1 T_a(x) \, dx/2 = 1
$$
Sketch:
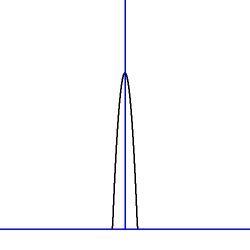
Example 7. $T(x) = $ finite at $x=0$ with compact support:
$$
T(x) = \begin{cases} 0 & \mbox{for} & -\infty < x < -1 \\
3/4.(1-x^2) & \mbox{for} & -1 < x < +1 \\
0 & \mbox{for} & +1 < x < +\infty \end{cases}
$$
Heuristics. Try an upside-down parabola with zeroes at $x=\pm 1$. It has the general form $\,y = a(1-x^2)$ .
Then calculate the integral:
$$
\int_{-\infty}^{+\infty} T(x) \, dx = \int_{-1}^{+1} a(1-x^2) \, dx =\\
a \left[x-\frac{1}{3}x^3\right]_{-1}^{+1} = 2a-\frac{2}{3}a = 1 \quad \Longrightarrow
\quad a = \frac{3}{4} \quad \mbox{Q.E.D.}
$$
Sketch:
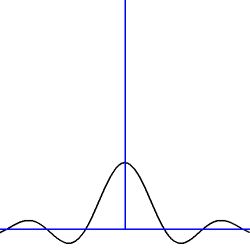
Example 8. $T(x) = \operatorname{sinc}(x)$ :
$$
T(x) = \frac{\sin(x)}{\pi x}
$$
The rest of this section is heuristics for calculating the normed integral.
High on the wish list of people who find Laplace transforms interesting is the
Laplace transform of a sine function:
$$
\int_0^{\infty} e^{-s x} \sin(x) \, dx = \mbox{??}
$$
We proceed by integrating by parts:
$$
\int_0^\infty e^{-s x} \sin(x) \, dx =
\int_0^\infty e^{-s x} d\left[ - \cos(x) \right] =
$$ $$
- \left[ e^{-s x} \cos(x) \right]_0^\infty
+ \int_0^\infty \cos(x) \, d \left[ e^{-s x} \right] =
1 - s \int_0^\infty e^{-s x} \cos(x) \, dx
$$
Feels good. Let's do it again:
$$
1 - s \int_0^\infty e^{-s x} \cos(x) \, dx =
1 - s \int_0^\infty e^{-s x} d \left[ \sin(x) \right] =
$$ $$
1 - s \left[ e^{-s x} \sin(x) \right]_0^\infty
+ s \, \int_0^\infty \sin(x) \, d \left[ e^{-s x} \right] =
$$ $$
1 - s^2 \, \int_0^\infty e^{-s x} \sin(x) \, d x =
\int_0^\infty e^{-s x} \sin(x) \, d x \quad \Longrightarrow
$$
Theorem. Laplace transform of sine:
$$
\int_0^\infty e^{-s x} \sin(x) \, dx = \frac{1}{1 + s^2}
$$
Theorem. Half area of $\operatorname{sinc}$ function:
$$
\int_0^\infty \operatorname{sinc}(x)\,dx = \frac{\pi}{2} \quad \Longrightarrow \quad
\int_{-\infty}^{+\infty} \frac{1}{\pi} \operatorname{sinc}(x)\, dx = 1
$$
Proof.
$$
\int_0^\infty \left[ \int_0^\infty e^{-s x} \sin(x) \, dx \right] \, ds =
\int_0^\infty \left[ \int_0^\infty e^{-s x} \sin(x) \, ds \right] \, dx
$$
Because iterated limits in the real world do always commute. Now we have a left
hand side and a right hand side. The left hand side, according to the above, is
equal to:
$$
\int_0^\infty \left[ \int_0^\infty e^{-s x} \sin(x) \, dx \right] \, ds =
\int_0^\infty \frac{ds}{1+s^2} = \left[ \arctan(s) \right]_0^\infty =
\frac{\pi}{2}
$$
The right hand side, on the other hand:
$$
\int_0^\infty \left[ \int_0^\infty e^{-s x} \sin(x) \, ds \right] \, dx =
\int_0^\infty \sin(x) \left[ \int_0^\infty e^{-s x} \, ds \right] \, dx =
$$ $$
\int_0^\infty \sin(x) \frac{1}{x} \left[ - e^{-y} \right]_0^\infty \, dx =
\int_0^\infty \frac{\sin(x)}{x} \, dx
$$
It finally follows that:
$$
\int_{-\infty}^\infty \frac{\sin(x)}{x} \, dx = \pi \qquad \mbox{Q.E.D.}
$$
Sketch:
Example 9. $T(x) = \operatorname{sinc}(x)$ squared:
$$
T(x) = \frac{1}{\pi} \left[\frac{\sin(x)}{x}\right]^2
$$
Calculating the normed integral:
$$
\int_0^\infty \left[\frac{\sin(x)}{x}\right]^2 dx = \int_0^\infty \sin^2(x)\, d\left(-\frac{1}{x}\right)=
-\left[\frac{\sin^2(x)}{x}\right]_0^\infty + \int_0^\infty \frac{2\sin(x)\cos(x)}{x} dx = \\
\int_0^\infty \frac{\sin(2x)}{2x} d(2x) = \frac{\pi}{2} \quad \Longrightarrow \quad
\int_{-\infty}^{+\infty} \frac{1}{\pi} \left[\frac{\sin(x)}{x}\right]^2 \, dx = 1
$$
Sketch:
THE END.








